【题目】如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为 . 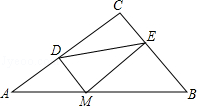
参考答案:
【答案】![]()
【解析】解:连接CM,如图所示: ∵MD⊥AC,ME⊥CB,
∴∠MDC=∠MEC=90°,
∵∠C=90°,
∴四边形CDME是矩形,
∴DE=CM,
∵∠C=90°,BC=3,AC=4,
∴AB= ![]() =
= ![]() =5,
=5,
当CM⊥AB时,CM最短,此时△ABC的面积= ![]() ABCM=
ABCM= ![]() BCAC,
BCAC,
∴CM的最小值= ![]() =
= ![]() ,
,
∴线段DE的最小值为 ![]() ;
;
所以答案是: ![]() .
.
【考点精析】关于本题考查的垂线段最短,需要了解连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用才能得出正确答案.
-
科目: 来源: 题型:
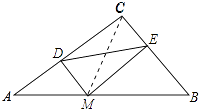
查看答案和解析>>【题目】如图(1),在△ABC中,∠C=90°,AB=5cm,BC=3cm,动点P在线段AC上以5cm/s的速度从点A运动到点C,过点P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△A′DP,设点P的运动时间为x(s).
(1)当点A′落在边BC上时,求x的值;
(2)在动点P从点A运动到点C过程中,当x为何值时,△A′BC是以A′B为腰的等腰三角形;
(3)如图(2),另有一动点Q与点P同时出发,在线段BC上以5cm/s的速度从点B运动到点C,过点Q作QE⊥AB于点E,将△BQE绕QE的中点旋转180°得到△B′EQ,连结A′B′,当直线A′B′与△ABC的一边垂直时,求线段A′B′的长.


-
科目: 来源: 题型:
查看答案和解析>>【题目】超市店庆促销,某种书包原价每个x元,第一次降价打“八折”,第二次降价每个又减10元,经两次降价后售价为90元,则得到方程( )
A.0.8x﹣10=90
B.0.08x﹣10=90
C.90﹣0.8x=10
D.x﹣0.8x﹣10=90 -
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2-9x+18=0的两个根是等腰三角形的底和腰,则这个三角形的周长为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论:①∠BOE=
 (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论(填编号). 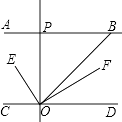
-
科目: 来源: 题型:
查看答案和解析>>【题目】在括号内填入适当的项:a﹣2b+3c=﹣().
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式x+3<2的解集是_____.
相关试题

