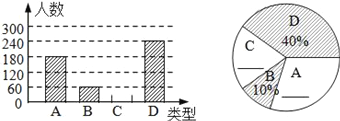
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,某食品厂为了解市民对去年销售量较好的肉馅粽、豆沙粽、红枣粽、蛋黄馅粽(以下分别用A,B,C,D表示这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?将不完整的条形图和扇形图补充完整;
(2)若居民区有8000人,请估计爱吃C ,D粽的总人数;
(3)若有外型完全相同的A,B,C,D粽各一个煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
参考答案:
【答案】(1)调查的居民数有600人; 条形图和扇形图补充见解析;(2)爱吃C, D粽的人数是4800人; (3)![]()
【解析】试题分析:(1)根据D类型的人数是240人,所占的比例是40%,据此即可求得总人数,利用总人数,减去其它各组的人数,即可求得C类的人数,据此即可完成直方图,算出A和C所占的百分比,即可补充扇形统计图;
(2)利用总人数8000乘以对应的百分比即可求解;
(3)利用列举法可以列举出所有的结果,然后利用概率公式即可求解.
试题解析:解:(1)调查的居民数有:240÷40%=600(人);C类的人数是:600﹣180﹣60﹣240=120(人),C类的人数所占的比例是: ![]() ×100%=20%,A类的人数所占的比例是:
×100%=20%,A类的人数所占的比例是: ![]() ×100%=30%.
×100%=30%.
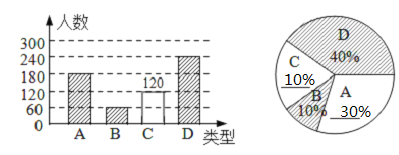
(2)爱吃C、D粽的人数是:8000×(20%+40%)=4800(人);
(3)画树状图如下:
 .
.
则P=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.

(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目供学生选择,为了估计全校学生对这四个活动项日的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中的一个项目),并把调查结果绘制成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
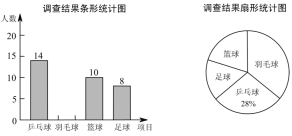
(1)求参加这次调查的学生人数,并补全条形统计图;
(2)求扇形统计图中“篮球”项目所对应扇形的圆心角度数;
(3)若该校共有1600名学生,试估计该校选择“足球”项目的学生有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送5批客人,行驶路程记录如下(规定向东为正,向西为负,单位:km):
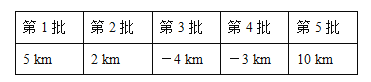
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过3km收费10元,超过3km的部分按每千米加1.8元收费,在这过程中该驾驶员共收到车费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”.例如,点P(1,4)的“3级关联点”为Q(3×1+4,1+3×4),即Q(7,13).
(1)已知点A(﹣2,6)的“
 级关联点”是点A1,点B的“2级关联点”是B1(3,3),求点A1和点B的坐标;
级关联点”是点A1,点B的“2级关联点”是B1(3,3),求点A1和点B的坐标;(2)已知点M(m﹣1,2m)的“﹣3级关联点”M′位于y轴上,求M′的坐标;
(3)已知点C(﹣1,3),D(4,3),点N(x,y)和它的“n级关联点”N′都位于线段CD上,请直接写出n的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E为AB上的点(不与A,B重合),△ADE与△FDE关于DE对称,作射线CF,与DE的延长线相交于点G,连接AG,

(1)当∠ADE=15°时,求∠DGC的度数;
(2)若点E在AB上移动,请你判断∠DGC的度数是否发生变化,若不变化,请证明你的结论;若会发生变化,请说明理由;
(3)如图2, 当点F落在对角线BD上时,点M为DE的中点,连接AM,FM,请你判断四边形AGFM的形状,并证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A、B在数轴上对应的数分别用+2、﹣6表示,P是数轴上的一个动点.

(1)数轴上A、B两点的距离为 .
(2)当P点满足PB=2PA时,求P点表示的数.
(3)将一枚棋子放在数轴上k0点,第一步从k点向右跳2个单位到k1,第二步从k1点向左跳4个单位到k2,第三步从k2点向右跳6个单位到k3,第四步从k3点向左跳8个单位到k4.
①如此跳6步,棋子落在数轴的k6点,若k6表示的数是12,则ko的值是多少?
②若如此跳了1002步,棋子落在数轴上的点k1002,如果k1002所表示的数是1998,那么k0所表示的数是 (请直接写答案).
相关试题

