Question

【题目】如图所示，平行四边形ABCD中，∠B=60°，将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转，且60°角的顶点始终与点C重合，角的两边所在的两直线分别交线段AB、AD于点E、F（不包括线段的端点）．

（1）问题发现：
如图1，若平行四边形ABCD为菱形，
试猜想线段AE、AF、AC之间的数量关系 ，请证明你的猜想．

（2）类比探究：
如图2，若AB：AD=1：2，过点C作CH⊥AD于点H，求AE：FH的比值；
（3）拓展延伸：
如图3，若AB：AD=1：4，请直接写出（AE+4AF）：AC的比值为 .

Answer 1

【答案】
（1）

AE+AF=AC

解：AE+AF=AC，理由如下：

∵四边形ABCD是平行四边形，∠BAD=120°，

∴∠D=∠B=60°，

∵四边形ABCD是菱形，

∴AD=AB，

∴△ABC，△ACD都是等边三角形，

∴∠B=∠CAD=60°，∠ACB=60°，BC=AC，

∵∠ECF=60°，

∴∠BCE+∠ACE=∠ACF+∠ACE=60°，

∴∠BCE=∠ACF，

在△BCE和△ACF中， ，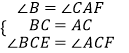

∴△BCE≌△ACF（ASA）．

∴BE=AF，

∴AE+AF=AE+BE=AB=AC；

故答案为：AE+AF=AC．

（2）

解设DH=x，由题意，CD=2x，CH= x，

∴AD=2AB=4x，

∴AH=AD﹣DH=3x，

∵CH⊥AD，

∴AC= =2 x，

∴AC2+CD2=AD2，

∴∠ACD=90°，

∴∠BAC=∠ACD=90°，

∴∠CAD=30°，

∴∠ACH=60°，

∵∠ECF=60°，

∴∠HCF=∠ACE，

∴△ACE∽△HCF，

∴AE：FH=AC：CH=2：1．

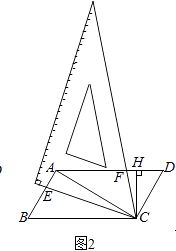
（3）

解：如图3中，作CN⊥AD于N，CM⊥BA于M，CM与AD交于点H．

∵∠ECF+∠EAF=180°，

∴∠AEC+∠AFC=180°，

∵∠AFC+∠CFN=180°，

∴∠CFN=∠AEC，∵∠M=∠CNF=90°，

∴△CFN∽△CEM，

∴ ，

∵ABCM=ADCN，AB：AD=1：4，

∴CM=4CN，

∴ = ，

设CN=a，FN=b，则CM=4a，EM=4b，

∵∠MAH=60°，∠M=90°，

∴∠AHM=∠CHN=30°，

∴HC=2a，HM=2a，HN= a，

∴AM= HM= a，AH=2AM= a，

∴AC= = a，

AE+4AF=（EM﹣AM）+4（AH+HN﹣FN）=EM﹣AM+4AH+4HN﹣4FN=4AH+4HN﹣AM= a，

∴ = = ；

故答案为： ．

【解析】（1）①先证明△ABC，△ACD都是等边三角形，再证明∠BCE=∠ACF即可解决问题．②根据①的结论得到BE=AF，由此即可证明．（2）设DH=x，由题意，CD=2x，CH= x，由△ACE∽△HCF，得 由此即可证明．（3）如图3中，作CN⊥AD于N，CM⊥BA于M，CM与AD交于点H．先证明△CFN∽△CEM，得出 ，由ABCM=ADCN，AD：AD=1：4，推出CM=4CN，得出 = ，设CN=a，FN=b，则CM=4a，EM=4b，再求出AC，AE+4AF，即可解决问题．
【考点精析】通过灵活运用勾股定理的概念和菱形的性质，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半即可以解答此题．