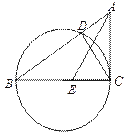
【题目】如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC.
(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC=![]() ,tan∠AEC=
,tan∠AEC=![]() ,求圆的直径.
,求圆的直径.
参考答案:
【答案】解: (1)∵BC是直径,∴∠BDC=90°,∴∠ABC+∠DCB=90°,
∵∠ACD=∠ABC,∴∠ACD+∠DCB=90°,∴BC⊥CA,∴CA是圆的切线.
(2)在Rt△AEC中,tan∠AEC=![]() ,∴
,∴![]() ,
, ![]() ;
;
在Rt△ABC中,tan∠ABC=![]() ,∴
,∴![]() ,
, ![]() ;
;
∵BC-EC=BE,BE=6,∴![]() ,解得AC=
,解得AC=![]() ,
,
∴BC=![]() .即圆的直径为10.
.即圆的直径为10.
【解析】试题分析:(1)根据圆周角定理BC得到∠BDC=90°,推出∠ACD+∠DCB=90°,即BC⊥CA,即可判断CA是圆的切线;
(2)根据锐角三角函数的定义得到tan∠AEC=![]() ,tan∠ABC=
,tan∠ABC=![]() ,推出AC=
,推出AC=![]() EC,BC=
EC,BC=![]() AC,代入BC﹣EC=BE即可求出AC,进一步求出BC即可.
AC,代入BC﹣EC=BE即可求出AC,进一步求出BC即可.
试题解析:(1)证明:∵BC是直径,
∴∠BDC=90°,
∴∠ABC+∠DCB=90°,
∵∠ACD=∠ABC,
∴∠ACD+∠DCB=90°,
∴BC⊥CA,∴CA是圆的切线.
(2)解:在Rt△AEC中,tan∠AEC=![]() ,
,
∴![]() ,AC=
,AC=![]() EC,
EC,
在Rt△ABC中,tan∠ABC=![]() ,
,
∴![]() ,BC=
,BC=![]() AC,
AC,
∵BC﹣EC=BE,BE=6,
∴![]() ,
,
解得: ![]() ,
,
∴BC=![]() =10,
=10,
答:圆的直径是10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BC边上的垂直平分线DE与边BC交于点D,边AB交于点E.若△EDC的周长为24,△ABC与四边形AEDC的周长之差为12,则线段DE的长为( )

A.12
B.6
C.24
D.36 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF.
(1)证明:△CBF≌△CDF;
(2)若AC=2
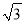 ,BD=2,求四边形ABCD的周长。
,BD=2,求四边形ABCD的周长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α=43°51′,则∠α的余角等于_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个单项式_____,使得它与3x2y的和仍是单项式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
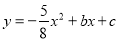 过A(1,0)、B(-1,-1)、C(3,m)三点。
过A(1,0)、B(-1,-1)、C(3,m)三点。(1)求抛物线的解析式及m的值;
(2)判断
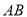 与AC的位置关系,并证明你的结论;
与AC的位置关系,并证明你的结论;(3)在抛物线上是否存在点P,当PH
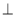 x轴于点H时,以P、H、A为顶点的三角形与
x轴于点H时,以P、H、A为顶点的三角形与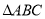 相似?若存在,求出点P坐标;若不存在,请说明理由。
相似?若存在,求出点P坐标;若不存在,请说明理由。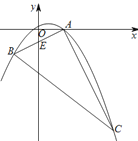
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上A、B、C三点对应的数分别是a、b、c,若ab<0,c为最大的负整数,c>a且|b|>|a|.
(1)请在数轴上标出A,B,C三点的大致位置;
(2)化简|a﹣b|+|b﹣a+c|﹣|b﹣c|.

相关试题

