【题目】对于二次函数y=﹣3(x+1)2﹣2的图象与性质,下列说法正确的是( )
A.对称轴是直线x=1,最小值是﹣2
B.对称轴是直线x=1,最大值是﹣2
C.对称轴是直线x=﹣1,最小值是﹣2
D.对称轴是直线x=﹣1,最大值是﹣2
参考答案:
【答案】D
【解析】
由二次函数的解析式可求得其最值及对称轴,可得答案.
解:∵y=﹣3(x+1)2﹣2,
∴抛物线开口向下,对称轴为x=﹣1,
∴当x=﹣1时,y有最大值﹣2,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若ax=2,ay=3,则ax+y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
-
科目: 来源: 题型:
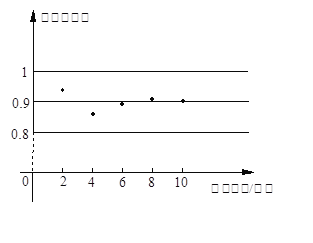
查看答案和解析>>【题目】某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:
⑴这种树苗成活的频率稳定在_________,成活的概率估计值为_______________.
⑵该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵;
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
投篮次数n
8
10
15
20
30
40
50
进球次数m
6
8
12
17
25
32
40
进球频

(1)计算并填写进球频率.
(2)这位运动员投篮一次,进球的概率约是多少(精确到0.1)?
(3)这位运动员投篮十次,必定会投进八球吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把抛物线y=2x2向左平移2个单位,再向上平移1个单位,所得到的抛物线的解析式为( )
A.y=2(x+2)2+1B.y=2(x+2)2﹣1
C.y=2(x﹣2)2﹣1D.y=2(x﹣2)2+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微笑的无花果,质量只有0.000000076克,将0.000000076克用科学记数法表示为( )
A.7.6×10﹣8
B.0.76×10﹣9
C.7.6×108
D.0.76×109
相关试题

