【题目】如图,在平面直角坐标系xOy中,直线y=x+4与坐标轴分别交于A、B两点,抛物线y=﹣x2+bx+c过A、B两点,点D为线段AB上一动点,过点D作CD⊥x轴于点C,交抛物线于点E.

(1)求抛物线的解析式.
(2)求△ABE面积的最大值.
(3)连接BE,是否存在点D,使得△DBE和△DAC相似?若存在,求出点D坐标;若不存在,说明理由.
参考答案:
【答案】(1)y=﹣x2﹣3x+4.(2)△ABE面积的最大值为8.(3)存在点D,使得△DBE和△DAC相似,点D的坐标为(﹣3,1)或(﹣2,2).
【解析】试题分析:(1)首先求出点A、B的坐标,然后利用待定系数法求出抛物线的解析式;
(2)设点C坐标为(m,0)(m<0),则点E坐标为(m,-m2-3m+4),从而得出OC=-m、OF=-m2-3m+4、BF=-m2-3m,根据S△ABE=S梯形AOFE-S△AOB-S△BEF得出S=-2(m+2)2+8,据此可得答案;
(3)由于△ACD为等腰直角三角形,而△DBE和△DAC相似,则△DBE必为等腰直角三角形.分两种情况讨论,要点是求出点E的坐标,由于点E在抛物线上,则可以由此列出方程求出未知数.
试题解析:(1)在直线解析式y=x+4中,令x=0,得y=4;令y=0,得x=﹣4,
∴A(﹣4,0),B(0,4).
∵点A(﹣4,0),B(0,4)在抛物线y=﹣x2+bx+c上,
∴![]() ,
,
解得:b=﹣3,c=4,
∴抛物线的解析式为:y=﹣x2﹣3x+4.
(2)如图,连接AE、过点E作EF⊥y轴于点F,
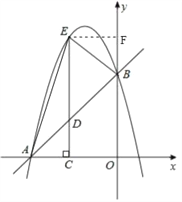
设点C坐标为(m,0)(m<0),则点E坐标为(m,﹣m2﹣3m+4),
则OC=﹣m,OF=﹣m2﹣3m+4,
∵OA=OB=4,
∴BF=﹣m2﹣3m,
则S△ABE=S梯形AOFE﹣S△AOB﹣S△BEF
=![]() ×(﹣m+4)(﹣m2﹣3m+4)﹣
×(﹣m+4)(﹣m2﹣3m+4)﹣![]() ×4×4﹣
×4×4﹣![]() ×(﹣m)×(﹣m2﹣3m).
×(﹣m)×(﹣m2﹣3m).
=﹣2m2﹣8m
=﹣2(m+2)2+8,
∵﹣4<m<0,
∴当m=﹣2时,S取得最大值,最大值为8.
即△ABE面积的最大值为8.
(3)设点C坐标为(m,0)(m<0),则OC=﹣m,CD=AC=4+m,BD=![]() OC=﹣
OC=﹣![]() m,
m,
则D(m,4+m).
∵△ACD为等腰直角三角形,△DBE和△DAC相似
∴△DBE必为等腰直角三角形.
i)若∠BED=90°,则BE=DE,
∵BE=OC=﹣m,
∴DE=BE=﹣m,
∴CE=4+m﹣m=4,
∴E(m,4).
∵点E在抛物线y=﹣x2﹣3x+4上,
∴4=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣3,
∴D(﹣3,1);
ii)若∠EBD=90°,则BE=BD=﹣![]() m,
m,
在等腰直角三角形EBD中,DE=![]() BD=﹣2m,
BD=﹣2m,
∴CE=4+m﹣2m=4﹣m,
∴E(m,4﹣m).
∵点E在抛物线y=﹣x2﹣3x+4上,
∴4﹣m=﹣m2﹣3m+4,解得m=0(不合题意,舍去)或m=﹣2,
∴D(﹣2,2).
综上所述,存在点D,使得△DBE和△DAC相似,点D的坐标为(﹣3,1)或(﹣2,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的平面直角坐标系中表示下面各点:
A(0,3);B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);G(5,0)
(1)A点到原点O的距离是 。
(2)将点C向
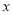 轴的负方向平移6个单位,它与点 重合。
轴的负方向平移6个单位,它与点 重合。(3)连接CE,则直线CE与
 轴是什么关系?
轴是什么关系?(4)点F分别到
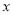 、
、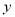 轴的距离是多少?
轴的距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在x轴上到原点距离为3的点的坐标为_______;在x轴上到点(-2,0)距离为5个单位的点的坐标是_______;在x轴上到点(-
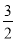 ,0)距离为4.5个单位的点的坐标是_______.
,0)距离为4.5个单位的点的坐标是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小方格都是长为1个单位的正方形.若学校位置的坐标为A(1,2),解答以下问题:
(1)请在图中建立适当的直角坐标系,并写出图书馆B位置的坐标;
(2)若体育馆位置的坐标为C(-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,
(1)A处是否会受到火车的影响,并写出理由
(2)如果A处受噪音影响,求影响的时间.

-
科目: 来源: 题型:
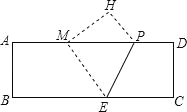
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
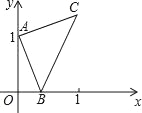
A.
 B.
B. 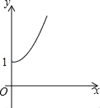 C.
C. 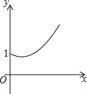 D.
D. 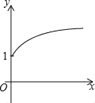
相关试题

