Question

【题目】已知：在中， ， 平分交于点，点在线段上（点不与点、重合），且．

（）如图，若，且，则__________， __________．

（）如图，①求证： ．

②若，且，求的度数．

Answer 1

【答案】（1）， ；（2）①见解析；②

【解析】试题分析：（1）由等腰三角形的性质得到∠EBC=∠ECB=27°，根据角平分线的性质得到∠DEB=∠EBC+∠ECB=54°，再由角平分线的性质得到∠ACD=∠ECB=27°，因为∠EAC=2∠EBC=54°，求得∠AEC=180°-27°-54°=99°；

（2）在CB上截取CF，使CF=CA，连接EF，构造全等三角形，由全等三角形的性质推出AE=FE，再根据FB=FE，得到AE=FB，即可得出AE+AC=FB+FC=BC；

（3）在CB上截取CF，使CF=CA，连接EF，连接AF，由∠ECB=30°，得到∠ACB=60°，于是推出△AFC是等边三角形，通过三角形全等得到∠EBC=∠FAE，由∠FAC=60°，得到∠EAC=2∠EBC=2∠FAE，于是得出∠EBC的度数．

试题解析：解：（1）∵EB=EC，∴∠EBC=∠ECB=27°，∴∠DEB=∠EBC+∠ECB=54°．

∵CD平分∠ACB，∴∠ACD=∠ECB=27°．

∵∠EAC=2∠EBC=54°，∴∠AEC=180°-27°-54°=99°．

故答案为：54°，99°．

（2）①证明：如图1，在BC上取一点M，使BM=ME，∴∠MBE=∠MEB．

∵∠EAC=2∠MBE，∠EMC=∠MBE+∠MEB=2∠MBE，∴∠EAC=∠EMC．

在△ACE与△MCE中，∵∠CAE=∠CME，∠ACE=∠MCE，CE=CE，∴△ACE≌△MCE(AAS)，∴AE=ME， AC =CM，∴AE=BM，∴BC=BM+CM=AE+AC．

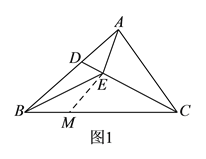
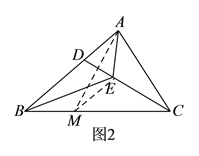
②如图2在BC上取一点M，使BM=ME，连接AM．

∵∠ECB=30°，∴∠ACB=60°，由①可知，△AMC是等边三角形（M点与B点重合），∴AM=AC=BE．

在△EMB与△MEA中，∵AE=BM，EM=EM，AM=BE，∴△EMB≌△MEA，∴∠EBC=∠MAE．

∵∠MAC=60°，∠EAC=2∠EBC=2∠MAE，∴∠MAE=20°，∠EAC=40°，∴∠EBC=20°．