【题目】已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴相交于点E,点B(-1,0),P是AC上的一个动点(P与点A、C不重合)
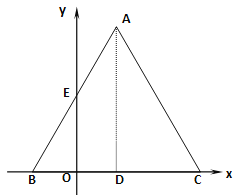
(1)求点A、E的坐标;
(2)若y=![]() 求过点A、E,求抛物线的解析式。
求过点A、E,求抛物线的解析式。
(3)连结PB、PD,设L为△PBD的周长,当L取最小值时,求点P的坐标及L的最小值,并判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由
参考答案:
【答案】(1)E(0,![]() )
)
(2)y=![]()
(3)在
【解析】解:(1)连结AD,不难求得A(1,2![]() )
)
OE=![]() ,得E(0,
,得E(0,![]() )
)
(2)因为抛物线y=![]() 过点A、E
过点A、E
由待定系数法得:c=![]() ,b=
,b=![]()
抛物线的解析式为y=![]()
(3)大家记得这样一个常识吗?
“牵牛从点A出发,到河边l喝水,再到点B处吃草,走哪条路径最短?”即确定l上的点P
方法是作点A关于l的对称点A',连结A'B与l的交点P即为所求.

本题中的AC就是“河”,B、D分别为“出发点”和“草地”。
由引例并证明后,得先作点D关于AC的对称点D',
连结BD'交AC于点P,则PB与PD的和取最小值,

即△PBD的周长L取最小值。
不难求得∠D'DC=30
DF=![]() ,DD'=2
,DD'=2![]()
求得点D'的坐标为(4,![]() )
)
直线BD'的解析式为:![]() x+
x+![]()
直线AC的解析式为:![]()
求直线BD'与AC的交点可得点P的坐标(![]() ,
,![]() )。
)。
此时BD'=![]() =/span>
=/span>![]() =2
=2![]()
所以△PBD的最小周长L为2![]() +2
+2
把点P的坐标代入y=![]() 成立,所以此时点P在抛物线上。
成立,所以此时点P在抛物线上。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列两个变量成反比例函数关系的是( )
①三角形底边为定值,它的面积S和这条边上的高线h;
②三角形的面积为定值,它的底边a与这条边上的高线h;
③面积为定值的矩形的长与宽;
④圆的周长与它的半径.
A.①④B.①③C.②③D.②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c、d是比例线段.a=2、b=3、d=6.那么c等于( )
A.9B.4C.1D.12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D、F分别在AB,AC上,DF垂直平分AB,E是BC的中点,若∠C=70°,则∠EDF=________
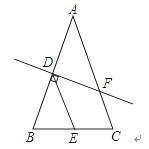
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:-1,0,1,2,3是它的一个样本,则这组数据的平均值大约是( )
A.5B.1C.-1D.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个数减去﹣5与2的和,所得的差是6,求该数的相反数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:a4a2= .
相关试题

