【题目】已知:如图,在正方形ABCD中,M,N分别是边AD,CD上的点,且∠MBN=45°,连接MN。
求证:MN=AM+CN.

参考答案:
【答案】证明见解析
【解析】先构造全等三角形,用得到的结论判断出△MBN≌△EBN,得出MN=EN,即可.
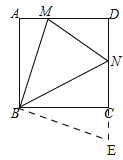
证明: 延长DC到E使CE=AM,连结BE
∵正方形ABCD,∴AB= BC,∠A=∠ABC=∠BCD=90。
∴∠BCE=∠A=90。∴△ABM≌△CBE,∴∠1=∠2,BM=BE,
∵∠MBN=45。∴∠1+∠3=45。∴∠2+∠3=45。
即∠EBN=∠MBN
∴△MBN≌△EBN,
∴MN=EN,∴MN=AM+CN.
“点睛”此题考查了正方形的性质,全等三角形的性质和判定,构造全等三角形是解答此题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC中,∠ABC=90°,点D在AC上,将△ABD绕顶点B沿顺时针方向旋转90°后得到△CBE.
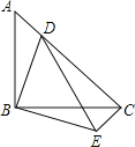
(1)求∠DCE的度数;
(2)当AB=8,AD∶DC=1∶3时,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只.某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
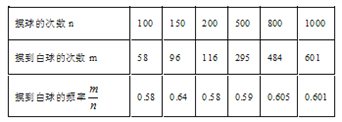
(1)请估计:当n很大时, 摸到白球的频率将会接近;
(2)假如你去摸一次, 摸到黑球的概率是;(本小题精确到0.1)
(3)试估算口袋中黑、白两种颜色的球各有多少只?
(4)解决了上面的问题,小明同学猛然顿悟,过去一个悬而未决的问题有办法了.这个问题是:在一个不透明的口袋里装有若干个白球,在不允许将球倒出来数的情况下,如何估计白球的个数(可以借助其他工具及用品)请你应用统计与概率的思想和方法解决这个问题,写出解决这个问题的主要步骤及估算方法.
-
科目: 来源: 题型:
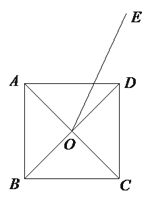
查看答案和解析>>【题目】如图,点O为正方形ABCD的对角线交点,将线段OE绕点O逆时针方向旋转
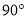 ,点E的对应点为点F,连接EF,AE,BF.
,点E的对应点为点F,连接EF,AE,BF.(1)请依题意补全图形;
(2)根据补全的图形,猜想并证明直线AE与BF的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值小于100的所有整数的和为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直接写出解集
-2x<8 _______;2x<8_______;2x<-8 _______;-2x<-8_______;
-
科目: 来源: 题型:
查看答案和解析>>【题目】“神舟十一号”载人飞船绕地球飞行了14圈,共飞行约590200km,则这个飞行距离用科学
记数法表示为( )
A. 59.02×104km B. 0.5902×106km C. 5.902×104km D. 5.902 ×105km
相关试题

