【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°
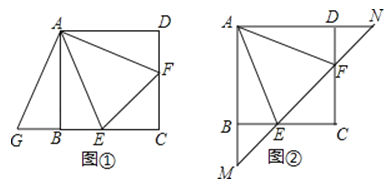
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2
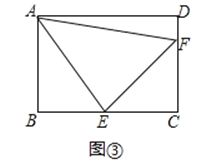
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)2(DF2+BE2)=EF2
【解析】
试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;
(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=![]() DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;
DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;
(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.
试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,
∴AF=AG,∠FAG=90°,
∵∠EAF=45°,
∴∠GAE=45°,
在△AGE与△AFE中,
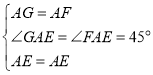 ,
,
∴△AGE≌△AFE;
(2)设正方形ABCD的边长为a.
将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.
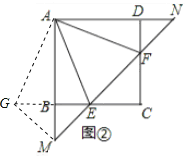
则△ADF≌△ABG,DF=BG.
由(1)知△AEG≌△AEF,
∴EG=EF.
∵∠CEF=45°,
∴△BME、△DNF、△CEF均为等腰直角三角形,
∴CE=CF,BE=BM,NF=![]() DF,
DF,
∴a-BE=a-DF,
∴BE=DF,
∴BE=BM=DF=BG,
∴∠BMG=45°,
∴∠GME=45°+45°=90°,
∴EG2=ME2+MG2,
∵EG=EF,MG=![]() BM=
BM=![]() DF=NF,
DF=NF,
∴EF2=ME2+NF2;
(3)EF2=2BE2+2DF2.
如图所示,延长EF交AB延长线于M点,交AD延长线于N点,
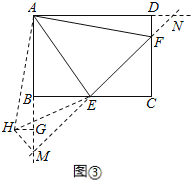
将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.
由(1)知△AEH≌△AEF,
则由勾股定理有(GH+BE)2+BG2=EH2,
即(GH+BE)2+(BM-GM)2=EH2
又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE-GH)2=EF2,
即2(DF2+BE2)=EF2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.

(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,△ABC的位置如图所示.
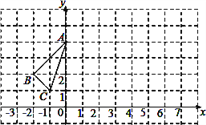
(1)请写出A、B、C三点的坐标;
(2)请求出△ABC的面积;
(3)将△ABC向右平移6个单位,再向上平移2个单位,请在图中作出平移后的△A′B′C′.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
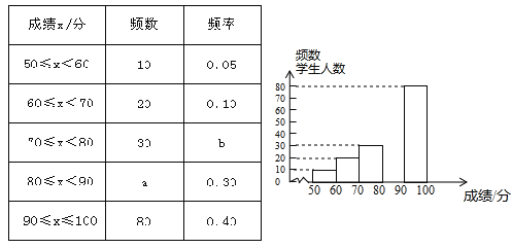
请根据所给信息,解答下列问题:
(1)a=________ , b=________ ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在________ 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有 人
-
科目: 来源: 题型:
查看答案和解析>>【题目】在烟台市举办的“读好书、讲礼仪”活动中,东华学校积极行动,各班图书角的新书、好书不断增多,除学校购买外,还有师生捐献的图书,下面是七年级(1)班全体同学捐献图书的情况统计图:
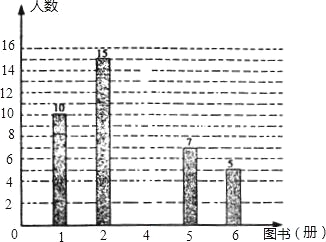
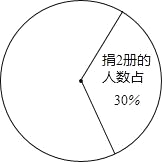
请你根据以上统计图中的信息,解答下列问题:
(1)该班有学生多少人?
(2)补全条形统计图;
(3)七(1)班全体同学所卷图书的中位数和众数分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知abc>0,a>c,ac<0,则a____0,b____0,c____0(选填“>”“<”或“=”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明因流感在医院观察,要掌握他在一周内的体温是否稳定,则医生需了解小明7天体温的( )
A. 众数 B. 方差 C. 平均数 D. 频数
相关试题

