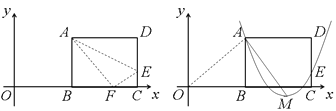
【题目】如图(1),矩形ABCD的一边BC在直角坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m>0.
(1)求点E、F的坐标(用含m的式子表示);(5分)
(2)连接OA,若△OAF是等腰三角形,求m的值;(4分)
(3)如图(2),设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值. (5分)
参考答案:
【答案】(1)∵四边形ABCD是矩形
∴AD=BC=10,AB=DC=8,∠D=∠DCB=∠ABC=90°
由折叠对称性:AF=AD=10,FE=DE
![]() ∴FC=4……………………………………2分
∴FC=4……………………………………2分
设EF=x,则EC=8-x
在Rt△ECF中,42+(8-x)2=x2解得x=5
∴CE=8-x=5
∵B (m,0) ∴E (m+10,3),F (m+6,0)……………………………………5分
(2)分三种情形讨论:
若AO=AF,∵AB⊥OF ∴OB=BF=6,∴m=6…………………………………7分
若OF=AF,则m+6=10 解得m=4
若AO=OF,在Rt△AOB中,AO2=OB2+AB2=m2+64

说明:求对一个m值得2分,求对二个m值得3分,求对三个m值得4分
(3)由(1)知A (m,8),E (m+10,3),
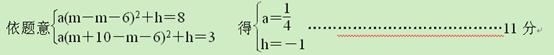 ∴M (m+6,-1)
∴M (m+6,-1)
设对称轴交AD于G
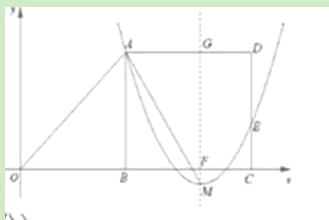
∴G (m+6,8) ∴AG=6,GM=8―(―1)=9
∵∠OAB+∠BAM=90°,∠BAM+∠MAG=90°,
∴∠OAB=∠MAG
又∠ABO=∠MGA=90°,
∴△AOB∽△AMG
![]() ∴m=12…………………………………14分
∴m=12…………………………………14分
【解析】略
-
科目: 来源: 题型:
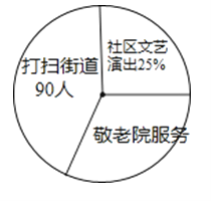
查看答案和解析>>【题目】今年3月5日,某中学组织六、七年级200位学生参与了“走出校门,服务社会”的活动,该校某数学学习小组的同学对那天参与打扫街道、敬老院服务和社区文艺演出的三组人数进行分别统计,部分数据如图所示:
(1)参与社区文艺演出的学生人数是________人,参与敬老院服务的学生人数是________人;
(2)该数学学习小组的同学还发现,六、七年级参与打扫街道的学生人数分别比参与敬老院服务的学生人数多了40%和60%,求参与敬老院服务的六、七年级学生分别有________人 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a+a=a2B.(2a)3=6a3C.(a-1)2=a2-1D.a3÷a=a2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,EF∥AC.
(1)求证:BE=AF;
(2)若∠ABC=60°,BD=12,求DE的长及四边形ADEF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解我县九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段统计如表:
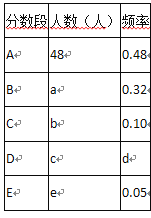
根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为________,c的值为________;
(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数”.请问甲同学体育成绩应在什么分数段内?________(填相应分数段的字母);
-
科目: 来源: 题型:
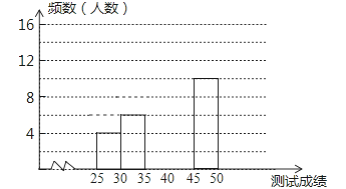
查看答案和解析>>【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别
成绩x分
频数(人数)
第1组
25≤x<30
4
第2组
30≤x<35
6
第3组
35≤x<40
14
第4组
40≤x<45
a
第5组
45≤x<50
10
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形既是轴对称图形,又是中心对称图形的是( )
A.
B.
C.
D.
相关试题

