Question

【题目】图中，AB为⊙O的直径，AB=4，P为AB上一点，过点P作⊙O的弦CD，设∠BCD=m∠ACD．

（1）已知 ，求m的值，及∠BCD、∠ACD的度数各是多少？
（2）在（1）的条件下，且 ，求弦CD的长；
（3）当 时，是否存在正实数m，使弦CD最短？如果存在，求出m的值，如果不存在，说明理由．

Answer 1

【答案】
（1）解：如图1，

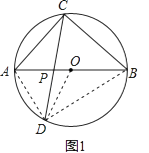
由 ，

得 m=2，
经检验m=2是原方程的根。

连结AD、BD

∵AB是⊙O的直径

∴∠ACB=90°，∠ADB=90°

又∵∠BCD=2∠ACD，∠ACB=∠BCD+∠ACD

∴∠ACD=30°，∠BCD=60°；

（2）解：如图1，连结AD、BD，则∠ABD=∠ACD=30°，AB=4

∴AD=2， ，

∵ ，

∴ ， ，

∵∠APC=∠DPB，∠ACD=∠ABD

∴△APC∽△DPB

∴ ，

∴ACDP=APDB= ×2 = ①，

PCDP=APBP= × = ②

同理△CPB∽△APD

∴ ，

∴BCDP=BPAD= ×2= ③，

由①得 ，由③得 ，

，

在△ABC中，AB=4，

∴ ，

∴

由② ，

得

∴

方法二：由①÷③得 ，

在△ABC中，AB=4，AC= × = ，

BC= ×2=

由③ ，

得

由② ，

得

∴ ；

（3）解：如图2，连结OD，

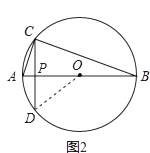
由 ，AB=4，

则 ，

则 ，

则 ，

要使CD最短，则CD⊥AB于点P

于是 ，

∵∠POD=30°

∴∠ACD=15°，∠BCD=75°

∴m=5，故存在这样的m值，且m=5．

【解析】（1）先求出此分式方程的解，即可求出∠BCD=2∠ACD，连结AD、BD、OD，根据两圆周角所夹弧对的两圆心角之和为180°，即可求出∠BCD、∠ACD的度数，或根据直径所对的圆周角是直角，得到∠ACB=∠BCD+∠ACD=90°，即可求得结果。
（2）由（1）可知∠ABD=30°，根据已知易求得AD、AP、BP、BD的长度，再证明△APC∽△DPB、△CPB∽△APD得出它们的对应边成比例，再在Rt△ABC中，根据勾股定理，求出DP的长，将DP的长代入② ，就可以求出PC的长，继而求出CD。方法二、由①÷③得 A C ： B C的值，根据AB=4求出BC的长，再由③和 ②，即可求出结果。
（3）要使弦CD最短，根据轴对称的相关知识，先找到点P的位置，即CD⊥AB于点P，连接OD，根据已知条件求出AP、OP的长，在Rt△POD中，运用锐角三角函数求出∠POD的度数，从而求出∠ACD，∠BCD的度数，即可求出m的值。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对圆周角定理的理解，了解顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半．