【题目】如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.

参考答案:
【答案】(1)见解析;(2)4
【解析】试题分析: (1)连接OB,由BD=CD,利用等边对等角得到∠DCB=∠DBC,再由AO垂直于OD,得到三角形AOC为直角三角形,得到两锐角互余,等量代换得到OB垂直于BD,即可得证;
(2)设BD=x,则OD=x+1,在RT△OBD中,根据勾股定理得出32+x2=(x+1)2,通过解方程即可求得.
试题解析:
(1)证明:连接OB,
∵OA=OB,DC=DB,
∴∠A=∠ABO,∠DCB=∠DBC,
∵AO⊥OD,
∴∠AOC=90°,即∠A+∠ACO=90°,
∵∠ACO=∠DCB=∠DBC,
∴∠ABO+∠DBC=90°,即OB⊥BD,
则BD为圆O的切线;
(2)解:设BD=x,则OD=x+1,而OB=OA=3,
在RT△OBD中,OB2+BD2=OD2,
即32+x2=(x+1)2,
解得x=4,
∴线段BD的长是4.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
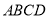 中,
中, ,
, ,点
,点 是
是 边的中点,点
边的中点,点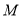 是
是 边上一动点(不与点
边上一动点(不与点 重合),延长
重合),延长 交射线
交射线 于点
于点 ,连接
,连接 ,
,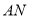 .
.
(1)求证:四边形
 是平行四边形;
是平行四边形;(2)填空:
①当
 的值为_______时,四边形
的值为_______时,四边形 是矩形;
是矩形;②当
 的值为______时,四边形
的值为______时,四边形 是菱形.
是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】感恩节即将来临,小王调查了初三年级部分同学在感恩节当天将以何种方式对帮助过自己的人表达感谢,他将调查结果分为如下四类:A类﹣﹣当面表示感谢、B类﹣﹣打电话表示感谢、C类﹣﹣发短信表示感谢、D类﹣﹣写书信表示感谢.他将调查结果绘制成了如图所示的扇形统计图和条形统计图.请你根据图中提供的信息完成下列各题:
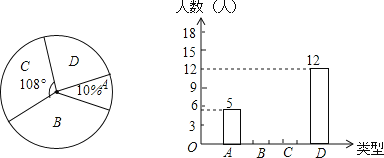
(1)补全条形统计图;
(2)在A类的同学中,有4人来自同一班级,其中有2人主持过班会.现准备从他们4人中随机抽出两位同学主持感恩节主题班会课,请用树状图或列表法求抽出1人主持过班会而另一人没主持过班会的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,请回答下列问题.
材料一:我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积,用现代式子表示即为:
 ①(其中
①(其中 为三角形的三边长,
为三角形的三边长, 为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”;
为面积),而另一个文明古国古希腊也有求三角形面积的“海伦公式”; ……②(其中
……②(其中 )
)材料二:对于平方差公式:
 公式逆用可得:
公式逆用可得: ,例:
,例:
(1)若已知三角形的三边长分别为4,5,7,请分别运用公式①和公式②,计算该三角形的面积;
(2)你能否由公式①推导出公式②?请试试,写出推导过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若两条平行线EF,MN与直线AB,CD相交,则图中共有同旁内角的对数为( )
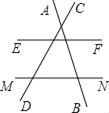
A. 4 B. 8 C. 12 D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,正方形
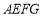 的两边分别在正方形
的两边分别在正方形 的边
的边 和
和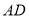 上,连接
上,连接 .填空:线段
.填空:线段 与
与 的数量关系为________;直线
的数量关系为________;直线 与
与 所夹锐角的大小为________.
所夹锐角的大小为________.


(2)如图②,将正方形
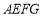 绕点
绕点 顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.
顺时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请说明理由.(3)把图②中的正方形都换成菱形,且
 ,如图③,直接写出
,如图③,直接写出 ______.
______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
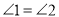 ,
,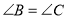 ,可推得
,可推得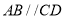 .理由如下:
.理由如下: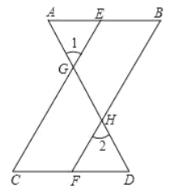
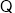
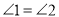 (已知),
(已知),且
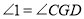 (________)
(________) 
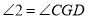 (等量代换)
(等量代换)
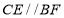 (________)
(________)
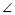 ________
________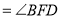 (________)
(________)又
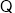
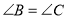 (已知)
(已知)
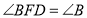 (等量代换)
(等量代换)
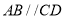 (________)
(________)
相关试题

