【题目】已知:关于x的一元二次方程x2﹣6x﹣m=0有两个实数根.
(1)求m的取值范围;
(2)如果m取符合条件的最小整数,且一元二次方程x2﹣6x﹣m=0与x2+nx+1=0有一个相同的根,求常数n的值.
参考答案:
【答案】(1)m≥﹣9;(2 )![]() .
.
【解析】试题分析:(1)根据判别式的意义得到△=(﹣6)2﹣4×1×(﹣m)≥0,然后解不等式即可得到m的范围;
(2)在(1)中m的取值范围内确定满足条件的m的值,再解方程x2﹣6x﹣m=0,然后把它的解代入x2+nx+1=0可计算出n的值.
试题解析:解:(1)根据题意得△=(﹣6)2﹣4×1×(﹣m)≥0,解得m≥﹣9;
(2)∵m≥﹣9,∴m的最小整数为﹣9,此时方程变形为x2﹣6x+9=0,解得x1=x2=3,把x=3代入x2+nx+1=0得9+3n+1=0,解得n=﹣![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b的图象与反比例函数y=
 的图象的两个交点;
的图象的两个交点;(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)求△AOB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程,解应用题
甲乙两人相约周末到影院看电影,他们的家分别距离影院1200米和2000米,两人分别从家中同时出发,已知甲和乙的速度比是
 ,结果甲比乙提前4分钟到达影院.
,结果甲比乙提前4分钟到达影院.(1)求甲、乙两人的速度?
(2)在看电影时,甲突然接到家长电话让其15分钟内赶回家,时间紧迫改变速度,比来时每分钟多走25米,甲是否能按要求时间到家?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某山是某市民周末休闲爬山的好去处,但总有些市民随手丢垃圾的情况出现.为了美化环境,提高市民的环保意识,某外国语学校某附属学校青年志愿者协会组织50人的青年志愿者团队,在周末前往临某森林公园捡垃圾.已知平均每分钟男生可以捡3件垃圾,女生可以捡2件垃圾,且该团队平均每分钟可以捡130件垃圾.请问该团队的男生和女生各多少人?
-
科目: 来源: 题型:
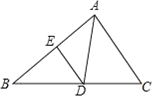
查看答案和解析>>【题目】如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.
(1)求证:△CAD∽△CBA;
(2)若BD=10,DC=8,求AC的长;
(3)在(2)的条件下,若DE∥AC,AE=4,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,矩形ABCD中,AB=
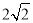 ,AD=4,在BC边上取点E,使BE=AB,将△ABE向左平移到△DCF的位置,得到四边形AEFD.
,AD=4,在BC边上取点E,使BE=AB,将△ABE向左平移到△DCF的位置,得到四边形AEFD.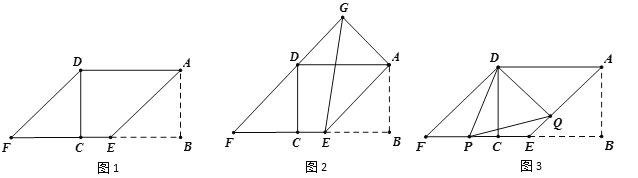
(1)求证:四边形AEFD是菱形;
(2)如图2,将△DCF绕点D旋转至△DGA,连接GE,求线段GE的长;
(3)如图3,设P、Q分别是EF、AE上的两点,且∠PDQ=67.5°,试探究线段PF、AQ、PQ之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,双曲线y1=
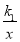 与直线y2=
与直线y2=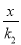 的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=
的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=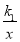 上的任意一点,且0<a<4.
上的任意一点,且0<a<4.(1)分别求出y1、y2的函数表达式;
(2)连接PA、PB,得到△PAB,若4a=b,求三角形ABP的面积;
(3)当点P在双曲线y1=
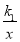 上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.
上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.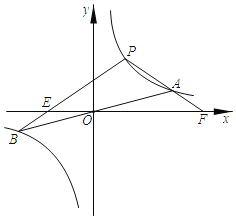
相关试题

