【题目】已知E,F分别是AB、CD上的动点,P也为一动点.
(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD; 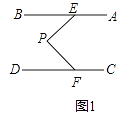
(2)如图2,若∠P=∠PFD﹣∠BEP,求证:AB∥CD; 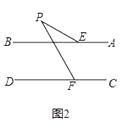
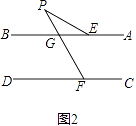
(3)如图3,AB∥CD,移动E,F使得∠EPF=90°,作∠PEG=∠BEP,求 ![]() 的值.
的值. 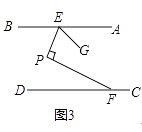
参考答案:
【答案】
(1)解:过P作PQ∥AB,

∵AB∥CD,
∴PQ∥CD,
∴∠BEP=∠1,∠2=∠PFD,
∵∠EPF=∠1+∠2,
∴∠EPF=∠BEP+∠PFD
(2)证明:∵∠BGP是△PEG的外角,
∴∠P=∠BGP﹣∠BEP.
∵∠P=∠PGB﹣∠BEP,
∴∠PFD=∠PGB,
∴AB∥CD
(3)解:由(1)的结论∠EPF=∠BEP+∠PFD=90°,
设∠PFD=x,则∠BEP=90°﹣x,
∵∠PEG=∠BEP=90°﹣x,
∴∠AEG=180°﹣2(90°﹣x)=2x,则 ![]() =
= ![]() =2
=2
【解析】(1)过P作PQ平行于AB,由AB与CD平行,得到PQ与CD平行,利用两直线平行内错角相等得到两对角相等,再由∠EPF=∠1+∠2,等量代换就可得证;(2)先根据三角形外角的性质得出∠P=∠BGP﹣∠BEP,再由∠P=∠PGB﹣∠BEP可知,∠PFD=∠PGB,由此可得出结论;(3)由(1)中的结论∠EPF=∠BEP+∠PFD,设设∠PFD=x,则∠BEP=90°﹣x,根据∠PEG=∠BEP=90°﹣x,利用平角定义表示出∠AEG,即可求出所求比值.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2014年吉林省对全省供热管网进行改造,改造后全年二氧化碳排放量共减少7620000吨,7620000这个数用科学记数法表示为( )
A.762×104
B.76.2×105
C.7.62×106
D.0.762×107 -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,O为坐标原点,已知点A(1,2),在y轴的正半轴上确定点P,使△AOP为等腰三角形,则点P的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,如果∠B=65°,∠A的外角等于130°,那么△ABC___(填“是”或“不是”)等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程x2﹣2x+c=0有两个相等的实数根,则c的值为( )
A.1
B.﹣1
C.4
D.﹣4 -
科目: 来源: 题型:
查看答案和解析>>【题目】下面关于投针实验的说法正确的是( )
A. 针与平行线相交和不相交的可能性是相同的
B. 针与平行线相交的概率与针的长度没有关系
C. 实验次数越多,估算针与平行线相交的概率越精确
D. 针与平行线相交的概率不受两平行线间距离的影响
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式的值:
(1)(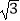 +
+ 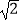 )﹣
)﹣ 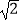
(2)(﹣3)2﹣|﹣ |+
|+  ﹣
﹣ 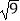
(3)x2﹣121=0
(4)(x﹣5)3+8=0.
相关试题

