【题目】如图:在△ABC中,CD是AB边上的高,AC=20,BC=15,DB=9. 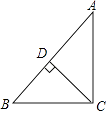
(1)求CD的长;
(2)△ABC是直角三角形吗?为什么?
参考答案:
【答案】
(1)解:∵CD⊥AB,
∴∠CDB=∠CDA=90°,
在Rt△BCD中,BC=15,DB=9,
根据勾股定理得:CD= ![]()
(2)解:△ABC为直角三角形,理由为:
在Rt△ACD中,AC=20,CD=12,
根据勾股定理得:AD= ![]() ;
;
∵AB=BD+AD=9+16=25,
∴AC2+BC2=AB2,
∴△ABC为直角三角形
【解析】(1)由CD垂直于AB,得到三角形BCD与三角形ACD都为直角三角形,由BC与DB,利用勾股定理求出CD的长;(2)三角形ABC为直角三角形,理由为:由BD+AD求出AB的长,利用勾股定理的逆定理得到三角形ABC为直角三角形.
【考点精析】认真审题,首先需要了解勾股定理的逆定理(如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB和CD的公共部分BD=
 AB=
AB=  CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】12﹣(﹣18)+(﹣7)﹣15.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东15°,射线OB的方向是北偏西40°,∠AOB=∠AOC,射线OD是OB的反向延长线.

(1)射线OC的方向是___________________;
(2)求∠COD的度数;
(3)若射线OE平分∠COD,求∠AOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=5x+b2-9的图象经过原点,则b=____.
-
科目: 来源: 题型:
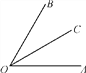
查看答案和解析>>【题目】已知:如图,OC是∠AOB的平分线.
(1)当∠AOB=60°时,求∠AOC的度数;
(2)在(1)的条件下,∠EOC=90°,请在图中补全图形,并求∠AOE的度数;
(3)当∠AOB=α时,∠EOC=90°,直接写出∠AOE的度数.(用含α的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图1.
①若∠AOC=60°,求∠DOE的度数;
②若∠AOC=α,直接写出∠DOE的度数(用含α的式子表示);
(2)将图1中的∠DOC绕点O顺时针旋转至图2的位置,试探究∠DOE和∠AOC的度数之间的关系,写出你的结论,并说明理由.

相关试题

