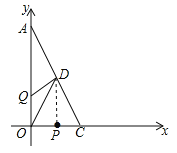
【题目】如图,以直角三角形![]() 的直角顶点
的直角顶点![]() 为原点,以
为原点,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴建立平面直角坐标系,点
轴建立平面直角坐标系,点![]() 满足
满足![]()
(1)则![]() 点的坐标为__________;
点的坐标为__________;![]() 点的坐标为____________.
点的坐标为____________.
(2)直角三角形![]() 的面积为_________.
的面积为_________.
(3)已知坐标轴上有两动点![]() 同时出发,
同时出发,![]() 点从
点从![]() 点出发沿
点出发沿![]() 轴负方向以1个单位长度每秒的速度匀速移动,
轴负方向以1个单位长度每秒的速度匀速移动,![]() 点从
点从![]() 点出发以2个单位长度每秒的速度沿
点出发以2个单位长度每秒的速度沿![]() 轴正方向移动,点
轴正方向移动,点![]() 到达
到达![]() 点整个运动随之结束。
点整个运动随之结束。![]() 的中点
的中点![]() 的坐标是
的坐标是![]() ,设运动时间为
,设运动时间为![]() 秒,问:是否存在这样的
秒,问:是否存在这样的![]() 使
使![]() ?若存在,请求出
?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

参考答案:
【答案】(1)(4,0),(0,8);(2)16;(3)t=2.
【解析】分析:(1)直接利用绝对值的性质结合二次根式的定义分析得出a,c的值,进而得出答案;
(2)根据三角形面积公式计算即可;
(3)首先得出CP=t,OP=4-t,OQ=2t,AQ=8-2t,再表示出△DOP和△DOQ的面积,进而得出等式求出答案.
详解:(1)∵![]() +|c﹣4|=0,∴c﹣4=0,a﹣2c=0,解得:c=4,a=8,∴C(4,0),A(0,8).
+|c﹣4|=0,∴c﹣4=0,a﹣2c=0,解得:c=4,a=8,∴C(4,0),A(0,8).
故答案为:(4,0),(0,8);
(2)直角三角形![]() 的面积=
的面积=![]() AO×OC=
AO×OC=![]() ×8×4=16;
×8×4=16;
(3)存在.由条件可知P点从C点运动到O点的时间为4秒,Q点从O点运动到A 点的时间为4秒,
∴当0<t≤4时,点Q在线段AO上,点P在线段OC上,
由题意可得:CP=t,OP=4-t,OQ=2t,AQ=8-2t,D(2,4), .
.
∵S△ODP=S△ODQ,∴8﹣2t=2t,∴解得:t=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列语句列出方程:
(1)比a小4的数是7:_____.
(2)3与x差的一半等于x的4倍______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知
 ,
, ,可得
,可得 =______;
=______;(2)如图2,在(1)的条件下,如果
 平分
平分 ,则
,则 =________;
=________;(3)如图3,在(1)(2)的条件下,如果
 ,则
,则 =_________;
=_________;(4)尝试解决下面问题:如图4,
 ,
, ,
, 是
是 的平分线,
的平分线, ,求
,求 的度数.
的度数.



-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生对三种国庆活动方案的意见,对该校学生进行了一次抽样调查(被调查学生至多赞成其中的一种方案),现将调查结果绘制成如图两幅不完整的统计图.

请根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了名学生;扇形统计图中方案1所对应的圆心角的度数为度;
(2)请把条形统计图补充完整;
(3)已知该校有1000名学生,试估计该校赞成方案1的学生约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】甲口袋中装有3个相同的小球,它们分别写有数值﹣1,1,5;乙口袋中装有3个相同的小球,它们分别写有数值﹣4,2,3.现从甲口袋中随机取一球,记它上面的数值为x,再从乙口袋中随机取一球,记它上面的数值为y.设点A的坐标为(x,y),请用树形图或列表法,求点A落在第一象限的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:

(1)该地出租车的起步价是元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元? -
科目: 来源: 题型:
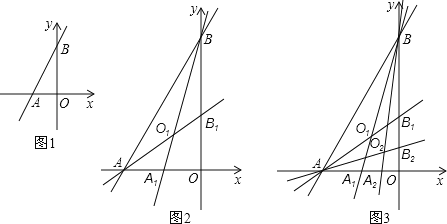
查看答案和解析>>【题目】如图1,一次函数y=2x+4与x轴,y轴分别相交于A,B两点,一次函数图象与坐标轴围成的△ABO,我们称它为此一次函数的坐标三角形.把坐标三角形面积分成相等的二部分的直线叫做坐标三角形的等积线.
(1)求此一次函数的坐标三角形周长以及过点A的等积线的函数表达式;
(2)如图2,我们把第一个坐标三角形△ABO记为第一代坐标三角形.第一代坐标三角形的等积线BA1,AB1记为第一对等积线,它们交于点O1,四边形A1OB1O1称为第一个坐标四边形.求点O1的坐标和坐标四边形A1OB1O1面积;
(3)如图3.第一对等积线与坐标轴构成了第二代坐标三角形△BA1O.△AOB1分别过点A,B作一条平分△BA1O,△AOB1面积的第二对等积线BA2,AB2,相交于点O2,如此进行下去.…,请直接写出On的坐标和第n个坐标四边形面积(用n表示).
相关试题

