【题目】A市和B市分别有库存的某联合收割机12台和6台,现决定开往C市10台和D市8台,已知从A市开往C市、D市的油料费分别为每台400元和800元,从B市开往C市和D市的油料费分别为每台300元和500元.
(1)设B市运往C市的联合收割机为x台,求运费w关于x的函数关系式.
(2)若总运费不超过9000元,问有几种调运方案?
(3)求出总运费最低的调运方案,并求出最低运费.
参考答案:
【答案】
(1)解:由题意可得,
w=400(10﹣x)+800(2+x)+300x+500(6﹣x)=200x+8600.
由 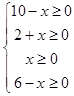 解得0≤x≤6.
解得0≤x≤6.
(2)解:由题意200x+8600≤9000,
解得x≤2,
∴x=0或1或2,
∴有三种调运方案:①B市运往C市的联合收割机为0台,B市运往D市的联合收割机为6台,A市运往C市的联合收割机为10台,A市运往D市的联合收割机为2台;
②B市运往C市的联合收割机为1台,B市运往D市的联合收割机为5台,A市运往C市的联合收割机为9台,A市运往D市的联合收割机为3台;
③B市运往C市的联合收割机为2台,B市运往D市的联合收割机为4台,A市运往C市的联合收割机为8台,A市运往D市的联合收割机为4台;
(3)解:∵w=200x+8600,
∵200>0,
∴w随x的增大而增大,
∵0≤x≤6,
∴x=0时,w最小,最小值为8600元.
【解析】(1)根据题意求出各个运费之和即可,利用不等式组确定自变量的取值范围即可.(2)列出不等式即可解决问题.(3)利用一次函数的增减性即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=k1x+b与反比例函数y=
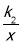 的图象交于第一象限内的P(
的图象交于第一象限内的P( ,8),Q(4,m)两点,与x轴交于A点.
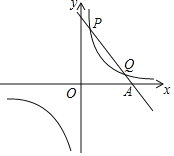
,8),Q(4,m)两点,与x轴交于A点.(1)分别求出这两个函数的表达式;
(2)写出点P关于原点的对称点P'的坐标;
(3)求∠P'AO的正弦值.
-
科目: 来源: 题型:
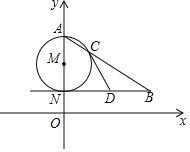
查看答案和解析>>【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解题过程,并解答后面的问题:
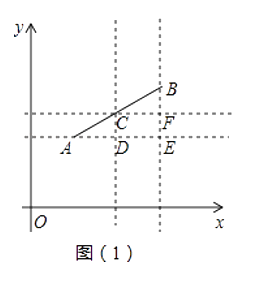
如图1,在平面直角坐标系xOy中,A(x1 , y1),B(x2 , y2),C为线段AB的中点,求C点的坐标.
解:分布过A、C做x轴的平行线,过B、C做y轴的平行线,两组平行线的交点如图1所示.
设C(x0 , y0),则D(x0 , y1),E(x2 , y1),F(x2 , y0)
由图1可知:x0=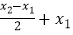 =
= 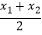
y0=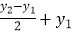 =
= 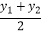
∴(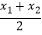 ,
, 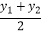 )
)
问题:
(1)已知A(﹣1,4),B(3,﹣2),则线段AB的中点坐标为
(2)平行四边形ABCD中,点A、B、C的坐标分别为(1,﹣4),(0,2),(5,6),求点D的坐标.
(3)如图2,B(6,4)在函数y= x+1的图象上,A(5,2),C在x轴上,D在函数y=
x+1的图象上,A(5,2),C在x轴上,D在函数y=  x+1的图象上,以A、B、C、D四个点为顶点构成平行四边形,直接写出所有满足条件的D点的坐标.
x+1的图象上,以A、B、C、D四个点为顶点构成平行四边形,直接写出所有满足条件的D点的坐标.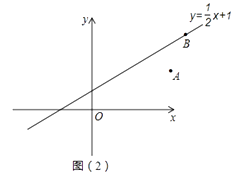
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式4x-5和3x-6的值相等,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:

根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
相关试题

