【题目】如图1是一张等腰直角三角形彩色纸,将斜边上的高线四等分,然后裁出三张宽度相等的长方形纸条,若恰好可以用这些纸条为一幅正方形美术作品镶边(纸条不重叠),则这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为( )
A.2:3
B.3:4
C.1:1
D.4:3
参考答案:
【答案】C
【解析】设三张宽度相等的长方形纸条的宽为x,则等腰直角三角形的高为4x,如图1, 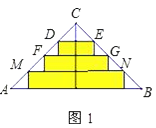
∴AB=8x,
∴S△ABC= ![]() 4x8x=16x2,
4x8x=16x2,
∵DE∥AB,FG∥AB,MN∥AB,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴DE= ![]() AB=2x,FG=4x,MN=6x,
AB=2x,FG=4x,MN=6x,
∴DE+FG+MN=2x+4x+6x=12x,∴镶嵌所得的作品的周长为12x=4x=16x,
∴镶嵌所得的作品的边长为4x,∴镶嵌所得的作品的面积=16x2,
∴这张彩色纸的面积与镶嵌所得的作品(如图2)面积之比为1:1.

所以答案是:C.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )

A.114°
B.123°
C.132°
D.147° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示.在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的中垂线,E、N在BC上,则∠EAN=( )

A. 58° B. 32° C. 36° D. 34°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难证明S1=S2+S3 .
(1) 如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(不必证明)
(2) 如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明;
(3) 若分别以直角三角形ABC三边为边向外作三个正多边形,其面积分别用S1、S2、S3表示,请你猜想S1、S2、S3之间的关系?.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
(1)在图中标出点D,并画出该四边形的另两条边;
(2)将四边形ABCD向下平移5个单位,画出平移后得到的四边形A1B1C1D1,并在对称轴AC上找出一点P,使PD+PD1的值最小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体的长为15宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )

A. 20 B. 25 C. 30 D. 32
相关试题

