【题目】阅读下面材料:
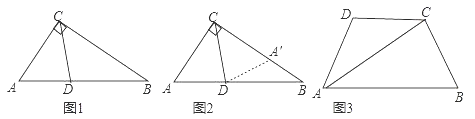
小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA′=CA,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).
请回答:
(1)在图2中,小明得到的全等三角形是△ ≌△ ;
(2)BC和AC、AD之间的数量关系是 .
参考小明思考问题的方法,解决问题:
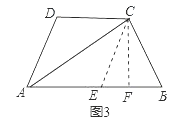
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9.求AB的长.
参考答案:
【答案】(1)ADC;A′DC;(2)BC=AC+AD;(3)21.
【解析】
试题分析:(1)由SAS容易证明△ADC≌△A′DC;
(2)由△ADC≌△A′DC,得出DA′=DA,∠CA′D=∠A=60°,再求出DA′=BA′,得出BA′=AD,即可得出结论;
解决问题:在AB上截取AE=AD,连接CE,先证明△ADC≌△AEC,得出AE=AD=9,CE=CD=10=BC,过点C作CF⊥AB于点F,设EF=BF=x;在Rt△CFB和Rt△CFA中,根据勾股定理求出x,即可得出结果.
试题解析:(1)△ADC≌△A′DC;理由如下:
∵CD平分∠ACB,
∴∠ACD=∠A′CD,
在△ADC和△A′DC中,
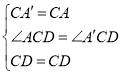 ,
,
∴△ADC≌△A′DC(SAS);
(2)BC=AC+AD;理由如下:
由(1)得:△ADC≌△A′DC,
∴DA′=DA,∠CA′D=∠A=60°,
∵∠ACB=90°,
∴∠B=90°-∠A=30°,
∵∠CA′D=∠B+∠BDA′,∠∠BDA′=30°=∠B,
∴DA′=BA′,
∴BA′=AD,
∴BC=CA′+BA′=AC+AD;
解决问题
如图,在AB上截取AE=AD,连接CE,如图3所示:
∵AC平分∠BAD,
∴∠DAC=∠EAC.
在△AEC和△ADC中,
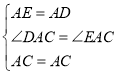 ,
,
∴△ADC≌△AEC(SAS),
∴AE=AD=9,CE=CD=10=BC,
过点C作CF⊥AB于点F,
∴EF=BF,
设EF=BF=x.
在Rt△CFB中,∠CFB=90°,由勾股定理得CF2=CB2-BF2=102-x2,
在Rt△CFA中,∠CFA=90°,由勾股定理得CF2=AC2-AF2=172-(9+x)2.
∴102-x2=172-(9+x)2,
解得:x=6,
∴AB=AE+EF+FB=9+6+6=21,
∴AB的长为21.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.

(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.
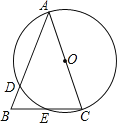
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
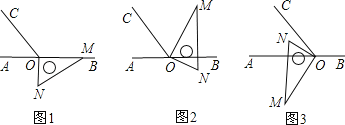
(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC.此时∠AOM= 度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.试探究∠AOM与∠NOC之间满足什么等量关系,并说明理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,是轴对称图形但不是中心对称图形的是( )
A.平行四边形 B.等腰三角形 C.矩形 D.正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条公路的转弯处是一段圆弧(
 ).
).(1)用直尺和圆规作出
 所在圆的圆心O;(要求保留作图痕迹,不写作法)
所在圆的圆心O;(要求保留作图痕迹,不写作法)(2)若
 的中点C到弦AB的距离为20m,AB=80m,求
的中点C到弦AB的距离为20m,AB=80m,求 所在圆的半径.
所在圆的半径.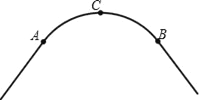
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△CDE中,已知AC=CD,AC⊥CD,∠B=∠E=90°,则下列结论不正确的是( )
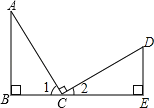
A.∠A与∠D互为余角
B.∠A=∠2
C.△ABC≌△CED
D.∠1=∠2
相关试题

