搜索
【题目】下列图形中，是轴对称图形但不是中心对称图形的是（ ）
A．平行四边形 B．等腰三角形 C．矩形 D．正方形
参考答案：
【答案】B.
【解析】
试题分析：根据轴对称图形的概念和中心对称图形的概念可得选项A，平行四边形不是轴对称图形，是中心对称图形，错误；选项B，等腰三角形是轴对称图形，不是中心对称图形，正确．选项C，矩形是轴对称图形，也是中心对称图形；错误；选项D，正方形是轴对称图形，也是中心对称图形，错误；故答案选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点D，交BC于点E．
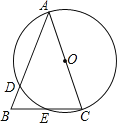
（1）求证：BE=CE；
（2）若BD=2，BE=3，求AC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，点O为直线AB上一点，过O点作射线OC，使∠BOC=120°，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．
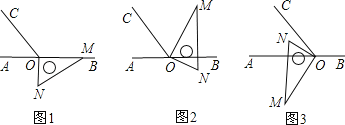
（1）如图2，将图1中的三角板绕点O逆时针旋转，使边OM在∠BOC的内部，且OM恰好平分∠BOC．此时∠AOM= 度；
（2）如图3，继续将图2中的三角板绕点O按逆时针方向旋转，使得ON在∠AOC的内部．试探究∠AOM与∠NOC之间满足什么等量关系，并说明理由；
（3）将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周，在旋转的过程中，若直线ON恰好平分∠AOC，则此时三角板绕点O旋转的时间是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
小明遇到这样一个问题：如图1，在Rt△ABC中，∠ACB=90°，∠A=60°，CD平分∠ACB，试判断BC和AC、AD之间的数量关系．
小明发现，利用轴对称做一个变化，在BC上截取CA′=CA，连接DA′，得到一对全等的三角形，从而将问题解决（如图2）．
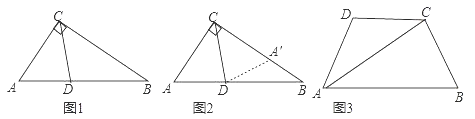
请回答：
（1）在图2中，小明得到的全等三角形是△ ≌△ ；
（2）BC和AC、AD之间的数量关系是 ．
参考小明思考问题的方法，解决问题：
如图3，在四边形ABCD中，AC平分∠BAD，BC=CD=10，AC=17，AD=9．求AB的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一条公路的转弯处是一段圆弧（
）．（1）用直尺和圆规作出
所在圆的圆心O；（要求保留作图痕迹，不写作法）（2）若
的中点C到弦AB的距离为20m，AB=80m，求所在圆的半径．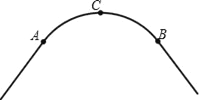
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC和△CDE中，已知AC=CD，AC⊥CD，∠B=∠E=90°，则下列结论不正确的是（ ）
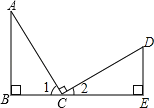
A．∠A与∠D互为余角
B．∠A=∠2
C．△ABC≌△CED
D．∠1=∠2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AB=AC，点D是BC边上的中点，点E在AD上，那么下列结论不一定正确的是（ ）
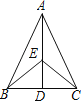
A．AD⊥BC B．∠EBC=∠ECB C．∠ABE=∠ACE D．AE=BE
相关试题
