Question

【题目】已知抛物线l：y=（x﹣h）2﹣4（h为常数）
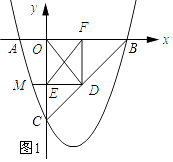
（1）如图1，当抛物线l恰好经过点P（1，﹣4）时，l与x轴从左到右的交点为A、B，与y轴交于点C．

①求l的解析式，并写出l的对称轴及顶点坐标．
②在l上是否存在点D，使S△ABD=S△ABC ， 若存在，请求出D点坐标，若不存在，请说明理由．
③点M是l上任意一点，过点M做ME垂直y轴于点E，交直线BC于点D，过点D作x轴的垂线，垂足为F，连接EF，当线段EF的长度最短时，求出点M的坐标．
（2）设l与双曲线y= 有个交点横坐标为x0 ， 且满足3≤x0≤5，通过l位置随h变化的过程，直接写出h的取值范围．

Answer 1

【答案】
（1）

解：①将P（1，﹣4）代入得：（1﹣h）2﹣4=﹣4，解得h=1，

∴抛物线的解析式为y=（x﹣1）2﹣4．

∴抛物线的对称轴为x=1，顶点坐标为（1，﹣4）．

②将x=0代入得：y=﹣3，

∴点C的坐标为（0，﹣3）．

∴OC=3．

∵S△ABD=S△ABC，

∴点D的纵坐标为3或﹣3．

当y=﹣3时，（x﹣1）2﹣4=﹣3，解得x=2或x=0．

∴点D的坐标为（0，﹣3）或（2，﹣3）．

当y=3时，（x﹣1）2﹣4=3，解得：x=1+ 或x=1﹣ ．

∴点D的坐标为（1+ ，3）或（1﹣ ，3）．

综上所述，点D的坐标为（0，﹣3）或（2，﹣3）或（1+ ，3）或（1﹣ ，3）时，S△ABD=S△ABC．

③如图1所示：

∵∠EOF=∠OED=∠OFD=90°，

∴四边形OEDF为矩形．

∴DO=EF．

依据垂线段的性质可知：当OD⊥BC时，OD有最小值，即EF有最小值．

把y=0代入抛物线的解析式得：（x﹣1）2﹣4=0，解得x=﹣1或x=3，

∴B（3，0）．

∴OB=OC．

又∵OD⊥BC，

∴CD=BD．

∴点D的坐标（ ，﹣ ）．

将y=﹣ 代入得：（x﹣1）2﹣4=﹣ ，解得x=﹣ +1或x= +1．

∴点M的坐标为（﹣ +1，﹣ ）或（ +1，﹣ ）

（2）

解：∵y=（x﹣h）2﹣4，

∴抛物线的顶点在直线y=﹣4上．

理由：对双曲线，当3≤x0≤5时，﹣3≤y0≤﹣ ，即L与双曲线在A（3，﹣3），B（5，﹣ ）之间的一段有个交点．

当抛物线经过点A时，（3﹣h）2﹣4=﹣3，解得h=2或h=4．

当抛物线经过点B时，（5﹣h）2﹣4=﹣ ，解得：h=5+ 或h=5﹣ ．

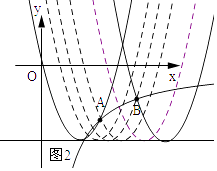
随h的逐渐增加，l的位置随向右平移，如图所示．

由函数图象可知：当2≤h≤5﹣ 或4≤h≤5+ 时，抛物线与双曲线在3≤x0≤5段有个交点

【解析】（1）①将P（1，﹣4）代入得到关于h的方程，从而可求得h的值，可得到抛物线的解析式，然后依据抛物线的解析式可直接得到抛物线的对称轴和顶点坐标；②先求得OC的长，然后由三角形的面积公式可得到点D的纵坐标为3或﹣3，最后将y的值代入求得对应的x的值即可；③先证明四边形OEDF为矩形，则DO=EF，由垂线的性质可知当OD⊥BC时，OD有最小值，即EF有最小值，然后由中点坐标公式可求得点D的坐标，然后可的点M的纵坐标，由函数的关系式可求得点M的横坐标；（2）抛物线y=（x﹣h）2﹣4的顶点在直线y=﹣4上，然后求得当x=3和x=5时，双曲线对应的函数值，得到点A和点B的坐标，然后分别求得当抛物线经过点A和点B时对应的h的值，然后画出平移后的图象，最后依据图象可得到答案．
【考点精析】通过灵活运用二次函数的图象和二次函数的性质，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小即可以解答此题．