【题目】解答题
(1)如图1,在圆内接正六边形ABCDEF中,半径OC=4,求正六边形的边长. 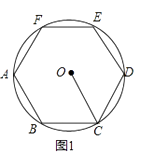
(2)如图2,在△ABC中,AB=13,BC=10,BC边上的中线AD=12.求证:AB=AC. 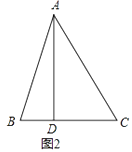
参考答案:
【答案】
(1)解:连接OD,如图所示:
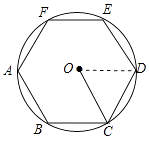
∵六边形ABCDEF是圆O的内接正六边形,
∴∠O= ![]() =60°,
=60°,
∵OC=OD,
∴△OCD是等边三角形,
∴CD=OC=4,
即正六边形的边长为4
(2)证明:∵AD是△ABC的中线,
∴BD=CD= ![]() BC=5,
BC=5,
∵AB=13,AD=12,
∴BD2+AD2=52+122=169=132=AB2,
∴△ABD是直角三角形,AD⊥BC,
又∵BD=CD,
∴AB=AC.
【解析】(1)连接OD,求出∠O=60°,证出△OCD是等边三角形,得出CD=OC=4即可;(2)由勾股定理的逆定理证出AD⊥BC,再由线段垂直平分线的性质即可得出AB=AC.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对正多边形和圆的理解,了解圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形ABCD的四个顶点A、B、C、D的坐标分别为(﹣1,1)、(﹣1,﹣3)、(5,3)、(1,3),则其对称轴的函数表达式为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】接下面各题
(1)解方程:x2+x﹣1=0
(2)抛物线y=﹣x2+bx+c经过点(1,0),(﹣3,0),求b、c的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.
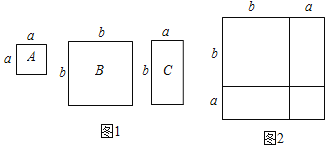
(1)请用两种不同的方法求图2大正方形的面积.
方法1: ;方法2:
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在植树节到来之际,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.
(1)若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?
(2)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】填空,完成下列说理过程:
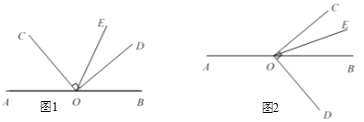
O是直线AB上一点,∠COD = 90°,OE平分∠BOC.
(1)如图1,若∠ AOC = 50°,求∠DOE的度数;
解:∵O是直线AB上一点,
∴∠AOC +∠BOC =180°.
∵∠AOC =50°,
∴∠BOC =130°.
∵OE平分∠BOC(已知),
∴∠COE =
 ∠BOC ( ).
∠BOC ( ).∴∠COE = °.
∵∠COD = 90°,∠DOE =∠ ∠ ,
∴∠DOE = °.
(2)将图1中∠ COD按顺时针方向转至图2所示的位置,OE仍然平分∠BOC.试猜想∠AOC与∠DOE的度数之间的关系为: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次方程解应用题:
2018年是我国改革开放40周年,改革开放是当代中国发展进步的必由之路,是实现中国梦的必由之路. 2018年10月20日在国家大剧院举行了《可爱的中国》庆祝改革开放40周年音乐会. 本次演出的票价分为以下几个类别,如下表所示:
演出票类别
A类
B类
C类
D类
E类
演出票单价(元/张)
300
280
240
180
100
小宇购买了A类和C类的演出票共10张,他发现这10张演出票的总价恰好可以购买8张B类票和4张E类票. 问小宇购买A类和C类的演出票各几张?
相关试题

