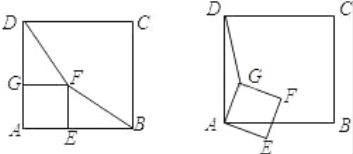
【题目】如图,正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1)连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题“在旋转的过程中,线段DF与BF的长始终相等”是否正确?答:___________。
(2)若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转过程中,你能否找到一条线段的长与线段DG的长始终相等?并以图为例说明理由.
参考答案:
【答案】(1)、不正确;(2)、DG=BE,证明过程见解析.
【解析】
试题分析:(1)、根据第二个图形就可以得出DF和BF不相等;(2)、根据正方形的性质得出AD=AB,AG=AE,∠DAG=∠BAE,从而得出△DAG和△BAE全等,从而得出DG=BE.
试题解析:(1)、不正确.
(2)、DG=BE
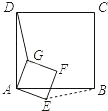
如图,∵四边形ABCD是正方形, ∴AD=AB,∵四边形GAEF是正方形,∴AG=AE,
又∵∠DAG+∠GAB=90°,∠BAE+∠GAB=90°, ∴∠DAG=∠BAE, ∴△DAG≌△BAE,
∴DG=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知今年甲的年龄比乙的年龄多12岁,4年后甲的年龄恰好是乙的年龄的2倍,则甲今年的年龄是( )
A. 20岁 B. 16岁 C. 15岁 D. 12岁
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,9,7,26,17,9.这组数据的众数是( )
A.17B.7C.16D.15
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A.6a+2a=8a2
B.(a﹣b)2=a2﹣b2
C.a4a6=a10
D.(a3)2=a5 -
科目: 来源: 题型:
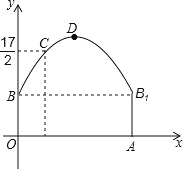
查看答案和解析>>【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣
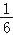 x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为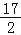 m.
m.(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式组
 的整数解共有4个,则a的取值范围是 ( )
的整数解共有4个,则a的取值范围是 ( )
A.6<a<7
B.6≤a<7
C.6≤a≤7
D.6<a≤7 -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,并写出整数解.
,并写出整数解.
相关试题

