【题目】如图,已知a∥b,长方形ABCD的点A在直线a上,B,C,D三点在平面上移动变化(长方形形状大小始终保持不变),请根据如下条件解答: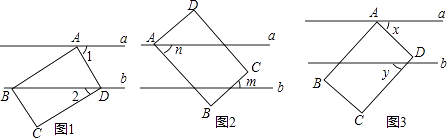
(1)图1,若点B、D在直线b上,点C在直线b的下方,∠2=30°,则∠1=;
(2)图2,若点D在直线a的上方,点C在平行直线a,b内,点B在直线b的下方,m,n表示角的度数,请写出m与n的数量关系并说明理由;
(3)图3,若点D在平行直线a,b内,点B,C在直线b的下方,x,y表示角的度数(x>y),且满足关系式x2﹣2xy+y2=100,求x的度数.
参考答案:
【答案】
(1)60°
(2)解:如图2,过C作EF∥a,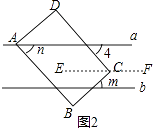
∵四边形ABCD是矩形,
∴AB∥CD,
∴n=∠4,
∵a∥b,EF∥a,
∴EF∥a∥b,
∴∠4=∠DCE ,∠ECB=m;
∴∠4+m=∠BCD=90°,
∴m+n=90°;
(3)解:如图3,过D作c∥b,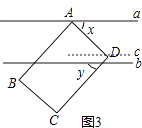
∵x2﹣2xy+y2=100,
∴(x﹣y)2=100,
∵x>y,
∴x﹣y=﹣10(舍去),
∴x﹣y=10,①
∵a∥b,c∥b,
∴a∥b∥c,
∵∠ADC=90°,
∴x+y=90,②
①+②得:x=50°.
【解析】(1)∵四边形ABCD是长方形,
∴∠ADC=90°,
∵∠2=30°,
∴∠ADB=60°,
∵a∥b,
∴∠1=∠ADB=60°,
故答案为:60°;
(1)根据矩形的四个角都是直角得出∠ADC=90°,根据角的和差得出∠ADB=60°,根据二直线平行内错角相等得出∠1=∠ADB=60°;
(2)过C作EF∥a,根据矩形的对边互相平行得出AB∥CD,根据二直线平行同位角相等得出n=∠4,根据平行于同一直线的两条直线互相平行得出EF∥a∥b,根据二直线平行,内错角相等得出∠4=∠DCE ,∠ECB=m;根据等式的性质得出结论;
(3)将方程x2﹣2xy+y2=100,利用直接开平方法得出x﹣y=10,①,根据平行于同一直线的两条直线互相平行得出a∥b∥c,根据二直线平行,内错角相等,及等式的性质得出结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】杭州市甲、乙两个有名的学校乐团,决定向某服装厂购买同样的演出服.如表是服装厂给出的演出服装的价格表:
购买服装的套数
1~39套(含39套)
40~69套(含69套)
70套及以上
每套服装的价格
80元
70元
60元
经调查:两个乐团共85人(甲乐团人数不少于46人),如果分别各自购买演出服,两个乐团共需花费6500元.请回答以下问题:
(1)如果甲、乙两个乐团联合起来购买服装,那么比各自购买服装最多可以节省多少元?
(2)甲、乙两个乐团各有多少名学生?
(3)现从甲乐团抽调a人,从乙乐团抽调b人(要求从每个乐团抽调的人数不少于5人),去儿童福利院献爱心演出,并在演出后每位乐团成员向儿童们进行“心连心活动”;甲乐团每位成员负责5位小朋友,乙乐团每位成员负责3位小朋友.这样恰好使得福利院65位小朋友全部得到“心连心活动”的温暖.请写出所有的抽调方案,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体没有曲面的是( )
A.圆锥
B.圆柱
C.球
D.棱柱 -
科目: 来源: 题型:
查看答案和解析>>【题目】“x与y的差的立方”用代数式表示为( )
A.x3﹣y
B.x﹣y3
C.x3﹣y3
D.(x﹣y)3 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
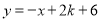 (k>0)与双曲线
(k>0)与双曲线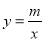 (x>0)交于点M、N,且点N的横坐标为k. .
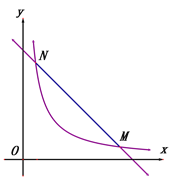
(x>0)交于点M、N,且点N的横坐标为k. .(1) 如图1,当k=1时.
①求m的值及线段MN的长;
②在y轴上是否是否存在点Q,使∠MQN=90°,若存在,请求出点Q的坐标;若不存在,请说明理由.
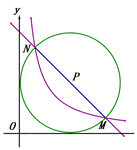
(2) 如图2,以MN为直径作⊙P,当⊙P与y轴相切时,求k值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=( )

A.90°
B.135°
C.270°
D.315° -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元,每上涨1元,则每个月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
相关试题

