【题目】A、B两城相距900千米,一辆客车从A城开往B城,车速为每小时80千米,同时一辆出租车从B城开往A城,车速为每小时100千米,设客车出发时间为t(小时).
探究 若客车、出租车距A城的距离分别为y1、y2,写出y1、y2关于t的函数关系式及自变量取值范围,并计算当y1=240千米时y2的値.
发现 (1)设点C是A城与B城的中点,AC=![]() AB,通过计算说明:哪个车先到达C城?该车到达C后再经过多少小时,另一个车会到达C?
AB,通过计算说明:哪个车先到达C城?该车到达C后再经过多少小时,另一个车会到达C?
(2)若两车扣相距100千米时,求时间t.
决策 已知客车和出租车正好在A,B之间的服务站D处相遇,此时出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种选择返回B城的方案:
方案一:继续乘坐出租车到C城,加油后立刻返回B城,出租车加油时间忽略不计;
方案二:在D处换乘客车返回B城.
试通过计算,分析小王选择哪种方式能更快到达B城?
参考答案:
【答案】探究:y1=80t(0≤t≤![]() ),y2=900﹣100t(0≤t≤9),y2=600;发现:(1)客车先到达C,再过2.25小时出租车到达;(2)两车相距100千米时,时间t为
),y2=900﹣100t(0≤t≤9),y2=600;发现:(1)客车先到达C,再过2.25小时出租车到达;(2)两车相距100千米时,时间t为![]() 或
或![]() 小时.决策:方案二更快.
小时.决策:方案二更快.
【解析】分析:探究:根据路程=速度×时间,即可得出y1、y2关于t的函数关系式,根据关系式算出y1=200千米时的时间t,将t代入y2的解析式中即可得出结论;
发现:(1)根据(1)中的函数关系式,令y=300即可分别算出时间t1和t2,二者做差即可得出结论;
(2)两车相距100千米,分两种情况考虑,解关于t的一元一次方程即可得出结论;
决策:根据时间=路程÷速度和,算出到达点D的时间,再根据路程=速度×时间算出AD、BD的长度,结合时间=路程÷速度,即可求出两种方案各需的时间,两者进行比较即可得出结论.
详解:探究:由已知得:y1=80t(0≤t≤![]() ),y2=900﹣100t(0≤t≤9),当y1=240时,即80t=240,∴t=3,∴y2=900﹣100×3=600;
),y2=900﹣100t(0≤t≤9),当y1=240时,即80t=240,∴t=3,∴y2=900﹣100×3=600;
发现:(1)∵AC=![]() AB=
AB=![]() 900=300km,∴客车到达C点需要的时间:80t1=300,解得:t1=3.75;
900=300km,∴客车到达C点需要的时间:80t1=300,解得:t1=3.75;
出租车到达C点需要的时间:900﹣100t2=300,解得:t2=6>3.75,6﹣3.75=2.25,∴客车先到达C,再过2.25小时出租车到达;
(2)两车相距100千米,分两种情况:
①y2﹣y1=100,即900﹣80t﹣100t=100,解得:t=![]() ;
;
②y1﹣y2=100,即80t﹣(900﹣100t)=100,解得:t=![]() .
.
综上可知:两车相距100千米时,时间t为![]() 或
或![]() 小时.
小时.
决策:两车相遇,即80t+100t=900,解得t=5,此时AD=80×5=400(千米),BD=900﹣400=500(千米).
方案一:t1=(2CD+BD)÷100=7(小时);
方案二:t2=500÷80=6.25(小时).
∵t1>t2,∴方案二更快.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列资料,解决问题:
定义:在分式中,对于只含有一个字母的分式,当分子的次数小于分母的次数时,我们称之为“真分式”,如:
 ,这样的分式就是真分式;当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如:
,这样的分式就是真分式;当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如: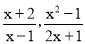 这样的分式就是假分式,假分式也可以化为带分式(即:整式与真分式的和的形式).
这样的分式就是假分式,假分式也可以化为带分式(即:整式与真分式的和的形式).如:
 .
.(1)分式
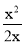 是 (填“真分式”或“假分式”);
是 (填“真分式”或“假分式”);(2)将假分式
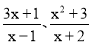 分别化为带分式;
分别化为带分式;(3)如果分式
 的值为整数,求所有符合条件的整数x的值.
的值为整数,求所有符合条件的整数x的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌饮水机厂生产一种饮水机和饮水机桶,饮水机每台定价350元,饮水机桶每只定价50元,厂方开展促销活动期间,可以同时向客户提供两种优惠方案:
方案一:买一台饮水机送一只饮水机桶;
方案二:饮水机和饮水机桶都按定价的90%付款.
现某客户到该饮水机厂购买饮水机30台,饮水机桶
 只(
只( 超过30).
超过30).(1)若该客户按方案一购买,求客户需付款(用含
 的式子表示);若该客户按方案二购买,求客户需付款(用含
的式子表示);若该客户按方案二购买,求客户需付款(用含 的式子表示);
的式子表示);(2)若
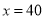 时,通过计算说明此时按哪种方案购买较为合算?
时,通过计算说明此时按哪种方案购买较为合算?(3)当
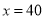 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数. -
科目: 来源: 题型:
查看答案和解析>>【题目】有四张规格、质地相同的卡片,它们背面完全相同,正面图案分别是A.平行四边形,B.菱形,C.矩形,D.正方形,将这四张卡片背面朝上洗匀后.
(1)随机抽取一张卡片图案是轴对称图形的概率是 ;
(2)随机抽取两张卡片(不放回),求两张卡片卡片图案都是轴对称图形的概率,并用树状图或列表法加以说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(3,﹣1),点A的坐标为(﹣2,
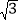 ),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.
),点B的坐标为(﹣3,0),点C在x轴上,且点D在点A的左侧.(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,同时菱形ABCD沿x轴向右以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与BC相切,且切点为BC的中点时,连接BD,求:
①t的值;
②∠MBD的度数;
(3)在(2)的条件下,当点M与BD所在的直线的距离为1时,求t的值.
-
科目: 来源: 题型:
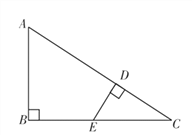
查看答案和解析>>【题目】如图,一艘军舰位于点A处,在其正南方向有一目标B,在点B的正东方向有一目标C,且AB+BC=3海里,在AC上有一艘补给船D,DC为1海里;军舰从点A出发,向AB,BC方向匀速航行,补给船同时从点D出发,沿垂直于AC方向匀速直线航行,欲将一批物品送达军舰.已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了几海里?
-
科目: 来源: 题型:
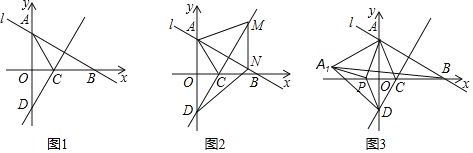
查看答案和解析>>【题目】如图1,在平面直角坐标系中,已知直线l:y
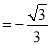 x+3交y轴于点A,x轴于点B,∠BAO的角平分线AC交x轴于点C,过点C作直线AB的垂线,交y轴于点D.
x+3交y轴于点A,x轴于点B,∠BAO的角平分线AC交x轴于点C,过点C作直线AB的垂线,交y轴于点D.(1)求直线CD的解析式;
(2)如图2,若点M为直线CD上的一个动点,过点M作MN∥y轴,交直线AB与点N,当四边形AMND为菱形时,求△ACM的面积;
(3)如图3,点P为x轴上的一个动点连接PA、PD,将△ADP沿DP翻折得到△A1DP,当以点A、A1、B为顶点的三角形是等腰三角形时,求点P的坐标.
相关试题

