【题目】如图,四边形ABCD是正方形,G是BC上任意一点(点G与B、C不重合),AE⊥DG于E,CF∥AE交DG于F.请你经过观察、猜测线段FC、AE、EF之间是否存在一定的数量关系?若存在,证明你的结论;若不存在,请说明理由.

参考答案:
【答案】AE=FC+EF,证明见解析.
【解析】分析:用AAS证明△AED≌△DFC,根据全等三角形有对应边相等得,AE=DF,DE=CF.
详解:AE=FC+EF,证明如下:
∵四边形ABCD是正方形,∴AD=DC,∠ADC=90度.
又∵AE⊥DG,CF∥AE,
∴∠AED=∠DFC=90°,∴∠EAD+∠ADE=∠FDC+∠ADE=90°,
∴∠EAD=∠FDC.
∴△AED≌△DFC(AAS).∴AE=DF,ED=FC.
∵DF=DE+EF,
∴AE=FC+EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:2﹣
 =2×
=2× +1,5﹣
+1,5﹣ =5×
=5× +1,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2,
+1,给出定义如下:我们称使等式a﹣b=ab+1的成立的一对有理数a,b为“共生有理数对”,记为(a,b),如:数对(2, ),(5,
),(5, ),都是“共生有理数对”.
),都是“共生有理数对”.(1)数对(﹣2,1),(3,
 )中是“共生有理数对”的是 ;
)中是“共生有理数对”的是 ;(2)若(m,n)是“共生有理数对”,则(﹣n,﹣m) “共生有理数对”(填“是”或“不是”);
(3)请再写出一对符合条件的“共生有理数对”为 ;(注意:不能与题目中已有的“共生有理数对”重复)
(4)若(a,3)是“共生有理数对”,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场同时购进甲、乙两种商品共
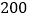 件,其进价和售价如右表,设其中甲种商品购进
件,其进价和售价如右表,设其中甲种商品购进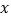 件.
件.(1)直接写出购进乙种商品的件数;(用含
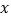 的代数式表示)
的代数式表示)(2)若设该商场售完这
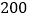 件商品的总利润为
件商品的总利润为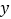 元.
元.①求
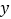 与
与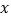 的函数关系式;
的函数关系式;②该商品计划最多投入
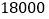 元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?
元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?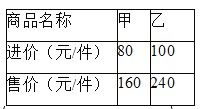
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,直线
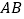 与
与 轴、
轴、 轴分别交于点
轴分别交于点 、点
、点 ,与双曲线
,与双曲线
 交于
交于 、
、 两点,分别过点
两点,分别过点 、点
、点 作
作 轴,
轴, 轴,垂足分别为点
轴,垂足分别为点 、点
、点 ,
,
(1)求线段
 的长;
的长;(2)若
 .
. ①求直线
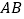 的解析式;
的解析式;②请你判断线段
 与线段
与线段 的大小关系,并说明理由.
的大小关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A、D两点表示的数分别为﹣5和6,且AC的中点为E,BD的中点为M,BC之间距点B的距离为
 BC的点N,则该数轴的原点为( )
BC的点N,则该数轴的原点为( )
A. 点E B. 点F C. 点M D. 点N
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.
(1)求证:四边形PMEN是平行四边形;
(2) 当AP为何值时,四边形PMEN是菱形?并给出证明。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.
(1)若AB=12 cm,则MN的长度是______cm;
(2)若AC=3 cm,CP=1 cm,求线段PN的长度.
相关试题

