Question

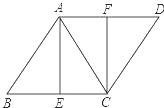
【题目】如图，已知菱形ABCD，AB=AC，E、F分别是BC、AD的中点，连接AE、CF．

（1）求证：四边形AECF是矩形；

（2）若AB=6，求菱形的面积．

Answer 1

【答案】（1）证明见解析；（2）18．

【解析】

试题分析：（1）首先证明△ABC是等边三角形，进而得出∠AEC=90°，四边形AECF是平行四边形，即可得出答案；

（2）利用勾股定理得出AE的长，进而求出菱形的面积．

试题解析：（1）∵四边形ABCD是菱形，

∴AB=BC，

又∵AB=AC，

∴△ABC是等边三角形，

∵E是BC的中点，

∴AE⊥BC，

∴∠AEC=90°，

∵E、F分别是BC、AD的中点，

∴AF=AD，EC=BC，

∵四边形ABCD是菱形，

∴AD∥BC且AD=BC，

∴AF∥EC且AF=EC，

∴四边形AECF是平行四边形，

又∵∠AEC=90°，

∴四边形AECF是矩形；

（2）在Rt△ABE中，AE=，

所以，S菱形ABCD=6×3=18．