【题目】阅读下面一段文字:
在数轴上点A,B分别表示数a,b.A,B两点间的距离可以用符号![]() 表示,利用有理数减法和绝对值可以计算A,B两点之间的距离
表示,利用有理数减法和绝对值可以计算A,B两点之间的距离![]() .
.
例如:当a=2,b=5时,![]() =5-2=3;当a=2,b=-5时,
=5-2=3;当a=2,b=-5时,![]() =
=![]() =7;当a=-2,b=-5时,
=7;当a=-2,b=-5时,![]() =
=![]() =3.综合上述过程,发现点A、B之间的距离
=3.综合上述过程,发现点A、B之间的距离![]() =
=![]() (也可以表示为
(也可以表示为![]() ).
).
请你根据上述材料,探究回答下列问题:
(1)数轴上表示1和3两点之间的距离是 ;
(2)表示数a和-2的两点间距离是6,则a= ;
(3)如果数轴上表示数a的点位于-4和3之间,求![]() 的值.
的值.
(4)是否存在数a,使代数式![]() 的值最小?若存在,请求出代数式的最小值,并直接写出数a的值或取值范围,若不存在,请简要说明理由.
的值最小?若存在,请求出代数式的最小值,并直接写出数a的值或取值范围,若不存在,请简要说明理由.
参考答案:
【答案】(1)2;(2)4或-8;(3)7;(4)2.
【解析】
(1)根据数轴的特点即可求解;
(2)根据题意得到![]() =6,即可求解;
=6,即可求解;
(3)根据A,B两点之间的距离![]() 即可求解;
即可求解;
(4)根据数轴上两点距离公式求出a的取值,即可求解.
解:(1)数轴上表示1和3两点之间的距离是3-1=2
故填:2;
(2)根据题意得到![]() =6,
=6,
即![]() =6
=6
∴a+2=±6
解得a=4或a=-8,
故填:4或-8;
(3)∵表示数a的点位于-4和3之间,
∴![]() =a+4,
=a+4,![]() =3-a.
=3-a.
∴![]() = a+4+3-a=7.
= a+4+3-a=7.
(4)代数式的值存在最小,
![]() 表示a到1,2,3的距离之和,
表示a到1,2,3的距离之和,
故当a=2时,![]() =1+0+1=2.
=1+0+1=2.
所以,最小值是2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知∠ABC=90°,∠CBD=30°,BP平分∠ABD,请补全图形,并求∠ABP的度数.
(2)在(1)的条件下,若∠ABC=α,∠CBD=β,直接写出∠ABP的度数.
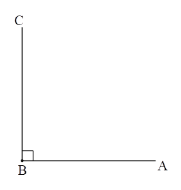
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过
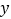 轴正半轴上的任意一点
轴正半轴上的任意一点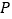 ,作
,作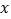 轴的平行线,分别与反比例函数
轴的平行线,分别与反比例函数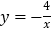 和
和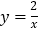 的图象交于点
的图象交于点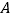 和点
和点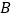 ,点
,点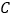 是
是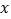 轴上一点,连接
轴上一点,连接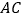 、
、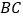 ,则
,则 的面积为( )
的面积为( )
A. 3B. 4C. 5D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
【答案】(1)A种型号的衣服每件90元,B种型号的衣服100元;(2)有三种进货方案,具体见解析.
【解析】试题分析:(1)等量关系为:A种型号衣服9件×进价+B种型号衣服10件×进价=1810,A种型号衣服12件×进价+B种型号衣服8件×进价=1880;
(2)关键描述语是:获利不少于699元,且A型号衣服不多于28件.关系式为:18×A型件数+30×B型件数≥699,A型号衣服件数≤28.
试题解析:(1)设A种型号的衣服每件x元,B种型号的衣服y元,
则:
 ,
,解之得
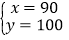 .
.答:A种型号的衣服每件90元,B种型号的衣服100元;
(2)设B型号衣服购进m件,则A型号衣服购进(2m+4)件,
可得:
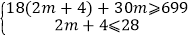 ,
,解之得192m12,
∵m为正整数,
∴m=10、11、12,2m+4=24、26、28.
答:有三种进货方案:
(1)B型号衣服购买10件,A型号衣服购进24件;
(2)B型号衣服购买11件,A型号衣服购进26件;
(3)B型号衣服购买12件,A型号衣服购进28件。
点睛:点睛:本题主要考查二元一次方程组和一元一次不等式组的实际问题的应用,解题的关键是读懂题目的意思,根据题目给出的条件,设出未知数,分别找出甲组和乙组对应的工作时间,找出合适的等量关系,列出方程组,再求解.
【题型】解答题
【结束】
21【题目】如图,锐角△ABC内接于⊙O,若⊙O的半径为6,sinA=
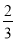 ,求BC的长.
,求BC的长.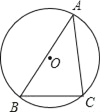
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数y=2x与反比例函数y=
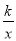 (k>0)的图象交于A、B两点,且点A的横坐标为4,
(k>0)的图象交于A、B两点,且点A的横坐标为4,(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
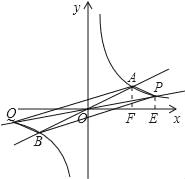
(3)过原点O的另一条直线l交双曲线y=
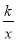 (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.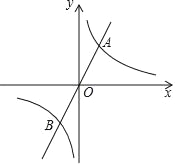
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正比例函数y=2x与反比例函数y=
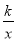 (k>0)的图象交于A、B两点,且点A的横坐标为4,
(k>0)的图象交于A、B两点,且点A的横坐标为4,(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=
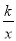 (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.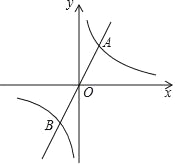
【答案】(1) k=32 (2) x<﹣8或0<x<8 (3) P(﹣7+3
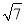 ,16+
,16+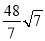 );或P(7+3
);或P(7+3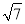 ,﹣16+
,﹣16+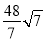 )
)【解析】分析:(1)先将x=4代入正比例函数y=2x,可得出y=8,求得点A(4,8),再根据点A与B关于原点对称,得出B点坐标,即可得出k的值;
(2)正比例函数的值小于反比例函数的值即正比例函数的图象在反比例函数的图象下方,根据图形可知在交点的右边正比例函数的值小于反比例函数的值.
(3)由于双曲线是关于原点的中心对称图形,因此以A、B、P、Q为顶点的四边形应该是平行四边形,那么△POA的面积就应该是四边形面积的四分之一即56.可根据双曲线的解析式设出P点的坐标,然后表示出△POA的面积,由于△POA的面积为56,由此可得出关于P点横坐标的方程,即可求出P点的坐标.
详解:(1)∵点A在正比例函数y=2x上,
∴把x=4代入正比例函数y=2x,
解得y=8,∴点A(4,8),
把点A(4,8)代入反比例函数y=
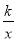 ,得k=32,
,得k=32,(2)∵点A与B关于原点对称,
∴B点坐标为(﹣4,﹣8),
由交点坐标,根据图象直接写出正比例函数值小于反比例函数值时x的取值范围,x<﹣8或0<x<8;
(3)∵反比例函数图象是关于原点O的中心对称图形,
∴OP=OQ,OA=OB,
∴四边形APBQ是平行四边形,
∴S△POA=S平行四边形APBQ×=
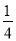 ×224=56,
×224=56,设点P的横坐标为m(m>0且m≠4),
得P(m,
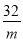 ),
),过点P、A分别做x轴的垂线,垂足为E、F,
∵点P、A在双曲线上,
∴S△POE=S△AOF=16,
若0<m<4,如图,
∵S△POE+S梯形PEFA=S△POA+S△AOF,
∴S梯形PEFA=S△POA=56.
∴
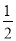 (8+
(8+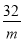 )(4﹣m)=56.
)(4﹣m)=56.∴m1=﹣7+3
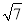 ,m2=﹣7﹣3
,m2=﹣7﹣3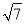 (舍去),
(舍去),∴P(﹣7+3
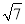 ,16+
,16+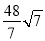 );
);若m>4,如图,
∵S△AOF+S梯形AFEP=S△AOP+S△POE,
∴S梯形PEFA=S△POA=56.
∴
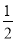 ×(8+
×(8+ )(m﹣4)=56,
)(m﹣4)=56,解得m1=7+3
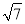 ,m2=7﹣3
,m2=7﹣3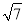 (舍去),
(舍去),∴P(7+3
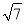 ,﹣16+
,﹣16+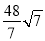 ).
).∴点P的坐标是P(﹣7+3
 ,16+
,16+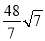 );或P(7+3
);或P(7+3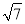 ,﹣16+
,﹣16+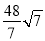 ).
).

点睛:本题考查了待定系数法求反比例函数与一次函数的解析式和反比例函数y=
 中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.利用数形结合的思想,求得三角形的面积.
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.利用数形结合的思想,求得三角形的面积.【题型】解答题
【结束】
23【题目】如图,在梯形ABCD中,AD∥BC,AB=DC=AD=9,∠ABC=70°,点E,F分别在线段AD,DC上(点E与点A,D不重合),且∠BEF=110°.
(1)求证:△ABE∽△DEF.
(2)当点E为AD中点时,求DF的长;
(3)在线段AD上是否存在一点E,使得F点为CD的中点?若存在,求出AE的长度;若不存在,试说明理由.

相关试题

