搜索
【题目】如图，过
轴正半轴上的任意一点
，作
轴的平行线，分别与反比例函数
和
的图象交于点
和点
，点
是轴上一点，连接
、
，则
的面积为（ ）
A. 3B. 4C. 5D. 6
参考答案：
【答案】A
【解析】
设P（0，b），由直线AB∥x轴，则A，B两点的纵坐标都为b，而A，B分别在反比例函数
和
的图象上，可得A点坐标为（-
，b），B点坐标为（
，b），从而求出AB的长，然后根据三角形的面积公式计算即可．
设P（0，b），
∵直线AB∥x轴，
∴A，B两点的纵坐标都为b，
∵点A在反比例函数的图象上，
∴当y=b，x=-，即A点坐标为（-，b），
又∵点B在反比例函数的图象上，
∴当y=b，x=，即B点坐标为（，b），
∴AB=-（-）=
，
∴S△ABC=
ABOP=b=3．
故选A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校初一年级两个班的学生要到航天科普教育基地进行社会大课堂活动，其中初一（1）班有40多人，初一（2）班有50多人，教育基地门票价格如下：
原计划两班都以班为单位分别购票，则一共应付1106元.请回答下列问题：
（1）初一（2）班有多少人？
（2）你作为组织者如何购票最省钱？比原计划省多少钱？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）已知∠ABC=90°，∠CBD=30°，BP平分∠ABD，请补全图形，并求∠ABP的度数.
（2）在（1）的条件下，若∠ABC=α，∠CBD=β，直接写出∠ABP的度数.
-
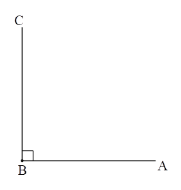
科目： 来源： 题型：
查看答案和解析>>【题目】某商场准备进一批两种不同型号的衣服，已知购进A种型号衣服9件，B种型号衣服10件，则共需1810元；若购进A种型号衣服12件，B种型号衣服8件，共需1880元；已知销售一件A型号衣服可获利18元，销售一件B型号衣服可获利30元，要使在这次销售中获利不少于699元，且A型号衣服不多于28件．
（1）求A、B型号衣服进价各是多少元？
（2）若已知购进A型号衣服是B型号衣服的2倍还多4件，则商店在这次进货中可有几种方案并简述购货方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面一段文字：
在数轴上点A，B分别表示数a，b.A，B两点间的距离可以用符号
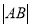表示，利用有理数减法和绝对值可以计算A，B两点之间的距离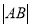.例如：当a=2，b=5时，
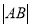=5-2=3；当a=2,b=-5时，=
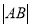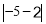=7；当a=-2，b=-5时，=
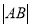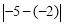=3.综合上述过程，发现点A、B之间的距离=
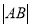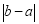(也可以表示为
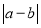).请你根据上述材料，探究回答下列问题：
（1）数轴上表示1和3两点之间的距离是 ；
（2）表示数a和-2的两点间距离是6，则a= ；
（3）如果数轴上表示数a的点位于-4和3之间，求
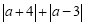的值.（4）是否存在数a，使代数式
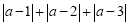的值最小？若存在，请求出代数式的最小值，并直接写出数a的值或取值范围，若不存在，请简要说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】某商场准备进一批两种不同型号的衣服，已知购进A种型号衣服9件，B种型号衣服10件，则共需1810元；若购进A种型号衣服12件，B种型号衣服8件，共需1880元；已知销售一件A型号衣服可获利18元，销售一件B型号衣服可获利30元，要使在这次销售中获利不少于699元，且A型号衣服不多于28件．
（1）求A、B型号衣服进价各是多少元？
（2）若已知购进A型号衣服是B型号衣服的2倍还多4件，则商店在这次进货中可有几种方案并简述购货方案．
【答案】（1）A种型号的衣服每件90元，B种型号的衣服100元；（2）有三种进货方案，具体见解析.
【解析】试题分析：（1）等量关系为：A种型号衣服9件×进价+B种型号衣服10件×进价=1810，A种型号衣服12件×进价+B种型号衣服8件×进价=1880；
（2）关键描述语是：获利不少于699元，且A型号衣服不多于28件．关系式为：18×A型件数+30×B型件数≥699，A型号衣服件数≤28．
试题解析：（1）设A种型号的衣服每件x元，B种型号的衣服y元，
则：
，解之得
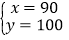.答：A种型号的衣服每件90元，B种型号的衣服100元；
（2）设B型号衣服购进m件,则A型号衣服购进(2m+4)件，
可得：
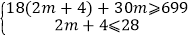，解之得192m12，
∵m为正整数，
∴m=10、11、12，2m+4=24、26、28.
答：有三种进货方案：
(1)B型号衣服购买10件，A型号衣服购进24件；
(2)B型号衣服购买11件，A型号衣服购进26件；
(3)B型号衣服购买12件，A型号衣服购进28件。
点睛：点睛：本题主要考查二元一次方程组和一元一次不等式组的实际问题的应用，解题的关键是读懂题目的意思，根据题目给出的条件，设出未知数，分别找出甲组和乙组对应的工作时间，找出合适的等量关系，列出方程组，再求解.
【题型】解答题
【结束】
21【题目】如图，锐角△ABC内接于⊙O，若⊙O的半径为6，sinA=
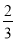，求BC的长．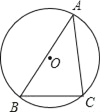
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知正比例函数y=2x与反比例函数y=
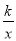（k＞0）的图象交于A、B两点，且点A的横坐标为4，（1）求k的值；
（2）根据图象直接写出正比例函数值小于反比例函数值时x的取值范围；
（3）过原点O的另一条直线l交双曲线y=
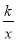（k＞0）于P、Q两点（P点在第一象限），若由点A、P、B、Q为顶点组成的四边形面积为224，求点P的坐标．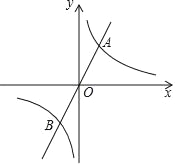
相关试题
