【题目】(1)在图①中以P为顶点画∠P,使∠P的两边分别和∠1的两边垂直;
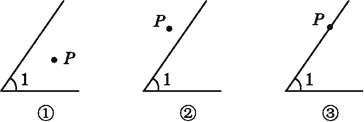
(2)量一量∠P和∠1的度数,它们之间的数量关系是 ;
(3)同样在图②和图③中以P为顶点作∠APB,使∠APB的两边分别和∠1的两边垂直,分别写出图②和图③中∠APB和∠1之间的数量关系(不要求写出理由).
图②: ,
图③: ;
(4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 (不要求写出理由).
参考答案:
【答案】(1)作图见解析;(2)∠1+∠P=180°;(3).∠1=∠APB;∠1=∠APB或∠1+∠APB=180°(4)相等或互补
【解析】试题分析:(1)根据题目要求,结合题中条件,由点P分别向∠1的两边做垂线,即可得到∠P;
(2)用量角器分别测量∠P与∠1的度数,即可得出二者的关系;
(3)分别在其余两图中,按要求作出∠P,再测量,即可得到结论;
(4)结合以上作图和结论,结合得到的∠P与∠1的关系,即可完成本题.
试题解析:(1)如图①,
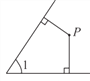
(2)测量可知∠+∠P=180°,所以∠1与∠P互补;
(3)如图②,图③,
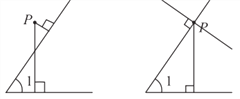
测量可知,图②中,∠1=∠P,所以图②中∠P与∠1相等;
图③中,结合角的表示可知由两个∠P,测量得到:∠1=∠P或∠+∠P=180°,所以图③中,∠P与∠1相等或互补.
(4)综上可知,如果一个角的两边分别和另一个角的两边垂直,那么这两个角相等或互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2a2)3的结果是_____.
-
科目: 来源: 题型:
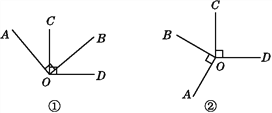
查看答案和解析>>【题目】已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD的度数.
(2)如图②,若∠BOC=60°,求∠AOD的度数.
(3)根据(1)(2)结果猜想∠AOD与∠BOC有怎样的关系?并根据图①说明理由.
(4)如图②,若∠BOC∶∠AOD=7∶29,求∠COB和∠AOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在图①中以P为顶点画∠P,使∠P的两边分别和∠1的两边垂直;
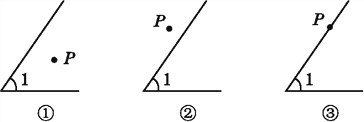
(2)量一量∠P和∠1的度数,它们之间的数量关系是 ;
(3)同样在图②和图③中以P为顶点作∠APB,使∠APB的两边分别和∠1的两边垂直,分别写出图②和图③中∠APB和∠1之间的数量关系(不要求写出理由).
图②: ,
图③: ;
(4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 (不要求写出理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为
 的中点,BE⊥CD垂足为E.
的中点,BE⊥CD垂足为E.
(1)求∠BCE的度数;
(2)求证:D为CE的中点;
(3)连接OE交BC于点F,若AB=
 ,求OE的长度.
,求OE的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】成都某学校团委为了解本校七年级500各学生的平均每晚的睡眠时间,随机选择了该年级100名学生进行调查.关于下列说法:
①本次调查方式属于抽样调查
②每个学生是个体
③100名学生是总体的一个样本
④总体是该校七年级500名学生的平均每晚的睡眠时间
共中正确的说法有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B两地相距20 km,甲、乙两人都从A地去B地,如图,l1和l2分别表示甲、乙两人所走路程s(km)与时间t(h)之间的关系,下列说法:①乙晚出发1 h;②乙出发3 h后追上甲;③甲的速度是4 km/h;④乙先到达B地.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
相关试题

