【题目】已知OA⊥OB,OC⊥OD.
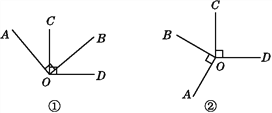
(1)如图①,若∠BOC=50°,求∠AOD的度数.
(2)如图②,若∠BOC=60°,求∠AOD的度数.
(3)根据(1)(2)结果猜想∠AOD与∠BOC有怎样的关系?并根据图①说明理由.
(4)如图②,若∠BOC∶∠AOD=7∶29,求∠COB和∠AOD的度数.
参考答案:
【答案】(1)130°;(2)120°;(3)互补;(4)∠COB=35°,∠AOD=145°.
【解析】试题分析:(1)根据垂线的定义,可得∠AOB与∠COD的度数,根据余角的定义,可得∠AOC,根据角的和差,可得答案;
(2)根据角的和差,可得答案;
(3)根据角的和差,可得答案;
(4)根据按比例分配,可得答案.
试题解析: (1)由OA⊥OB,OC⊥OD,
得∠AOB=∠COD=90°,
由余角的定义,得∠AOC=∠AOB∠BOC=90°50°=40°,
由角的和差,得∠AOD=∠AOC+∠COD=40°+90°=130°;
(2)由OA⊥OB,OC⊥OD,得∠AOB=∠COD=90°,
由角的和差,得∠AOD=360°∠AOB∠BOC∠COD=360°90°60°90°=120°,
(3)∠AOD+∠BOC=180,
∠AOD+∠BOC=130°+50°=180°;
(4)由角的和差,得∠AOD+∠BOC=360°∠AOB∠COD=180°,
按比例分配,得∠BOC=180°×![]() =35°
=35°
∠AOD=180°×![]() =145°.
=145°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列是一元二次方程的是( )
A.x2﹣2x﹣3=0B.x﹣2y+1=0C.2x+3=0D.x2+2y﹣10=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下4个有理数中,最小的是( )
A.﹣1
B.1
C.﹣2
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2a2)3的结果是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在图①中以P为顶点画∠P,使∠P的两边分别和∠1的两边垂直;
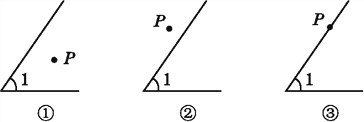
(2)量一量∠P和∠1的度数,它们之间的数量关系是 ;
(3)同样在图②和图③中以P为顶点作∠APB,使∠APB的两边分别和∠1的两边垂直,分别写出图②和图③中∠APB和∠1之间的数量关系(不要求写出理由).
图②: ,
图③: ;
(4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 (不要求写出理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)在图①中以P为顶点画∠P,使∠P的两边分别和∠1的两边垂直;
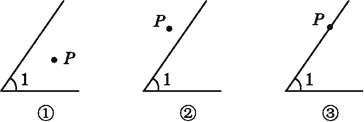
(2)量一量∠P和∠1的度数,它们之间的数量关系是 ;
(3)同样在图②和图③中以P为顶点作∠APB,使∠APB的两边分别和∠1的两边垂直,分别写出图②和图③中∠APB和∠1之间的数量关系(不要求写出理由).
图②: ,
图③: ;
(4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角 (不要求写出理由).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O的内接四边形ACDB中,AB为直径,AC:BC=1:2,点D为
 的中点,BE⊥CD垂足为E.
的中点,BE⊥CD垂足为E.
(1)求∠BCE的度数;
(2)求证:D为CE的中点;
(3)连接OE交BC于点F,若AB=
 ,求OE的长度.
,求OE的长度.
相关试题

