【题目】如图,将圆心角都是90°的扇形OAB和扇形OCD叠放在一起,连接AC、BD.
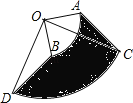
(1)将△AOC经过怎样的图形变换可以得到△BOD?
(2)若![]() 的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
的长为πcm,OD=3cm,求图中阴影部分的面积是多少?
参考答案:
【答案】(1)将△AOC绕点O顺时针旋转90°可以得到△BOD;(2)![]() π(cm2).
π(cm2).
【解析】
试题分析:(1)根据旋转的定义求解;
(2)先利用弧长公式计算出OA=2,再根据旋转的性质得到△AOC≌△BOD,则S△AOC=S△BOD,接着根据S△AOC+S扇形COD=S△BOD+S扇形AOB+S阴影部分得到S阴影部分=S扇形COD﹣S扇形AOB,然后利用扇形的面积公式计算即可.
解:(1)∵扇形OAB和扇形OCD的圆心角都是90°,
∴OA=OB,OC=OD,∠AOB=∠COD=90°,
∴将△AOC绕点O顺时针旋转90°可以得到△BOD;
(2)∵![]() =π,
=π,
∴OA=2,
∵△AOC绕点O顺时针旋转90°可以得到△BOD,
∴△AOC≌△BOD,
∴S△AOC=S△BOD,
∵S△AOC+S扇形COD=S△BOD+S扇形AOB+S阴影部分,
∴S阴影部分=S扇形COD﹣S扇形AOB=![]() ﹣
﹣![]() =
=![]() π(cm2).
π(cm2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(2a+b)2-(3a-b)2+5a(a-b),其中a =1,b=—1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下面不能判断是平行四边形的是( )
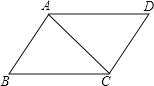
A.∠B=∠D,∠A=∠C
B.AB∥CD,AD∥BC
C.AB∥CD,AB=CD
D.∠B+∠DAB=180°,∠B+∠BCD=180°
-
科目: 来源: 题型:
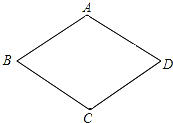
查看答案和解析>>【题目】已知ABCD的一组邻边AB、AD的长是关于x的方程x2﹣4x+m=0的两个实根.
(1)当m为何值时,四边形ABCD是菱形?
(2)在第(1)问的前提下,若∠ABC=60°,求ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,正确的是( )
A. t5·t5 = 2t5 B. t4+t2 = t 6 C. t3·t4 = t12 D. t2·t3 = t5
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算﹣5+2的结果是( )
A.﹣7 B.﹣3 C.3 D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有2个完全相同的小球,分别标有数字﹣1,﹣2.现从甲袋中随机抽取一个小球,将标有的数字记录为x,再从乙袋中随机抽取一个小球,将标有的数字记录为y,确定点M的坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在二次函数y=x2﹣2x﹣2的图象上的概率.
相关试题

