【题目】思考题:在对某地区的一次人口抽样统计分析中,各年龄段(年龄为整数)的人数如下表所示:
年龄段 | 0~9 | 10~19 | 20~29 | 30~39 | 40~49 | 50~59 | 60~69 | 70~79 | 80~89 |
人数 | 9 | 11 | 17 | 18 | 17 | 12 | 8 | 6 | 2 |
根据此表回答下列问题:
(1)样本中年龄在60岁以上(含60岁)的频率是多少?
(2)如果该地区现有人口80000人,为关注人口老龄化问题,请估算该地区60岁以上(含60岁)的人口数.
参考答案:
【答案】解:(1)根据题意,得:
样本中年龄在60岁以上(含60岁)的频率是![]() =0.16;
=0.16;
(2)根据(1),得:
80000×0.16=12800(人).
【解析】(1)根据表格,求得总人数,再根据频率=频数÷总数,进行计算;
(2)根据(1)的结论,能够用样本估计总体.
【考点精析】解答此题的关键在于理解频数与频率的相关知识,掌握落在各个小组内的数据的个数为频数;每一小组的频数与数据总数(样本容量n)的比值叫做这一小组的频率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市约有108000名应届初中毕业生,则数据108000用科学记数法表示为( )
A.0.108×106
B.1.08×105
C.1.08×106
D.1.1×105 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2a+3b=5ab
B.2a﹣3b=﹣1
C.2a2b﹣2ab2=0
D.2ab﹣2ba=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:

(1)写出题中的变量;
(2)写出点M的实际意义;
(3)求第1小时内,y与t的一次函数表达式;
(4)已知第5﹣6小时是小强妈妈做晚餐的时间,厨房内油烟导致PM2.5浓度升高.若该净化器吸收PM2.5的速度始终不变,则第6小时之后,预计经过多长时间室内PM2.5浓度可恢复正常? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级共有150名男生,从中随机抽取30名男生在“阳光体育活动”启动日进行“引体向上”测试,下表是测试成绩记录(单位:个):
3
2
1
2
3
3
5
2
2
4
2
4
2
5
2
3
4
4
1
3
3
2
5
1
4
2
3
1
2
4
(1)我们已经会列频数分布表、画条形统计图、折线统计图和扇形统计图.为了能让体育老师一目了然知道整个测试情况,请你选择一种合适的统计表或统计图整理表示上述数据;
(2)观察分析(1)中的统计表或统计图,请你写出两条从中获得的信息:
(3)规定八年级男生“引体向上”4个及以上为合格.若学校准备对“引体向上”不合格的男生提出锻炼建议,试估计要对八年级多少名男生提出这项建议? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,平行于x轴的直线与抛物线y=ax(a>0)相交于A、B两点.设点B的横坐标为m(m>0).
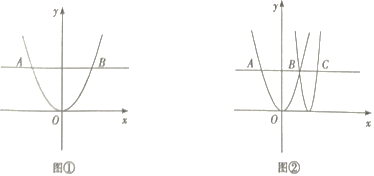
(1)求AB的长(用含m的代数式表示).
(2)如图②,点C在直线AB上,点C的横坐标为2m.若a=1,m=2,求顶点在x轴上且经过B、C两点的抛物线的顶点坐标.
(3)点D在直线AB上,BD=2AB,过O、B、D三点的抛物线的顶点为P,其对应函数的二次项系数为a1.
①求
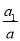 的值.
的值.②当m=2,△BPD为等腰直角三角形,直接写出a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校“沥园文学”社成员来自初一、初二、初三三个年级的学生,其人数比为2:3:5,如图所示的扇形图表示上述分布情况.已知来自初一的学生为10人,则下列说法不正确的是( )
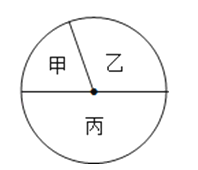
A.扇形甲的圆心角是72°
B.学生的总人数是90人
C.初三的人数比初二的人数多10人
D.初一的人数比初三的人数少15人
相关试题

