【题目】把正整数1,2,3,…,2018排成如图所示的7列,规定从上到下依次为第1行、第2行、第3行、…,从左到右依次为第1至7列.
(1)数2018在第______行第______列;
(2)按如图所示的方法用方框框出四个数,这四个数的和能否为296?如果能,求出这四个数;如果不能,请说明理由.

参考答案:
【答案】(1)289;2;(2)不能框出四个数的和为296;理由见解析.
【解析】
(1)由2018=288×7+2,可得出2018在第289行第2列;
(2)设被框的四个数中,最小的一个数为x,那么其余三个数分别为x+1、x+7、x+8,假设这四个数的和能为296,根据四个数之和为296即可得出关于x的一元一次方程,解方程可求出x的值,由x在第7列可得出假设不成立,此题得解.
解:(1)∵2018=288×7+2,
∴2018在第289行第2列.
故答案为289;2.
(2)设被框的四个数中,最小的一个数为x,那么其余三个数分别为x+1、x+7、x+8,
假设这四个数的和能为296,则
x+(x+1)+(x+7)+(x+8)=296,
解得:x=70.
∵70=10×7,
∴70在第7列,
∴这四个数不可能在同一方框中,
∴假设不成立,即按如图所示的方法不可能框出四个数的和为296.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,
 ,F是AD的中点,作
,F是AD的中点,作 ,垂足E在线段上,连接EF、CF,则下列结论
,垂足E在线段上,连接EF、CF,则下列结论 ;
; ;
; ,
, 中一定成立的是______
中一定成立的是______  把所有正确结论的序号都填在横线上
把所有正确结论的序号都填在横线上

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, ,
, 点P从A点出发沿
点P从A点出发沿 路径向终点运动,终点为B点;点Q从B点出发沿
路径向终点运动,终点为B点;点Q从B点出发沿 路径向终点运动,终点为A点
路径向终点运动,终点为A点 点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作
点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作 于E,
于E, 于
于 问:点P运动多少时间时,
问:点P运动多少时间时, 与QFC全等?请说明理由.
与QFC全等?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1 000元;经粗加工后销售,每吨利润可达4 500元;经精加工后销售,每吨利润涨至7 500元.
当地一家蔬菜公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司制订了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,添加下列条件仍然不能使ABCD成为菱形的是( )
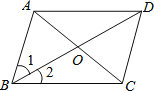
A. AB=BC B. AC⊥BD C. ∠ABC=90° D. ∠1=∠2
-
科目: 来源: 题型:
查看答案和解析>>【题目】武汉市光谷实验中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),下列说法错误的是( )

A. 九(1)班的学生人数为40 B. m的值为10
C. n的值为20 D. 表示“足球”的扇形的圆心角是70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a、b相交于点O,∠1=50°,点A在直线a上,直线b上存在点B,使以点O、A、B为顶点的三角形是等腰三角形,这样的B点有( )
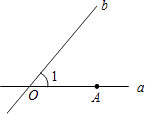
A.1个
B.2个
C.3个
D.4个
相关试题

