【题目】(1)平面上有四个点A,B,C,D,按照以下要求作图:
①作直线AD;
②作射线CB交直线AD于点E;
③连接AC,BD交于点F;
(2)图中共有 条线段;
(3)若图中F是AC的一个三等分点,AF<FC,已知线段AC上所有线段之和为18,求AF长.
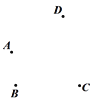
参考答案:
【答案】(1)画图见解析;(2)12;(3)AF=3.
【解析】
(1)根据语句作图即可;
(2)每条直线上有3条线段,一共4条直线,共有12条线段;
(3)设AF=x,依题意知,CF=2x,AC=3x,根据“线段AC上所有线段之和为18”列方程求解即可.
(1)如图所示;
(2) 每条直线上有3条线段,一共4条直线,共有12条线段.故答案为:12;
(3)设AF=x,依题意知,CF=2x,AC=3x,∴x+2x+3x=18,解得:x=3,∴AF=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A为中心将腰AB顺时针旋转90°至AE,连接DE,则△ADE的面积等于( )
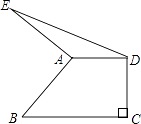
A.10
B.11
C.12
D.13 -
科目: 来源: 题型:
查看答案和解析>>【题目】用火柴棒按下图的方式搭塔式三角形,第一个图用了3根火柴棒,第二个图用了9根火柴棒,第三个图用了18根火柴棒,......,照这样下去,第9个图用了_____根火柴棒.
 ……
…… -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:
①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形;④S四边形ABMD=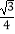 AM2 .
AM2 .
其中正确结论的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
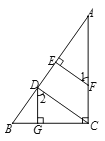
查看答案和解析>>【题目】如图所示,已知:DG⊥BC,AC⊥BC,FE⊥AB,∠1=∠2.
求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直的定义)
∴DG∥AC( )
∴∠2=∠DCA( )
∵∠1=∠2(已知)
∴∠1= (等量代换)
∴ (同位角相等,两直线平行)
∴ =∠ADC( )
∵EF⊥AB(已知), ∴∠AEF=90°( ),∴∠ADC=90° ,
∴CD⊥AB(垂直的定义)
-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细阅读下列材料.
“分数均可化为有限小数或无限循环小数”,反之,“有限小数或无限小数均可化为分数”.
例如:
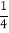 =1÷4=0.25;
=1÷4=0.25;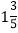 =
=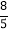 =8÷5=1.6;
=8÷5=1.6; =1÷3=
=1÷3= ,反之,0.25=
,反之,0.25=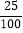 =
=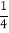 ;1.6=
;1.6=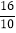 =
=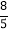 =
=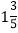 .那么
.那么 ,
,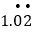 怎么化成分数呢?
怎么化成分数呢?解:∵
 ×10=3+
×10=3+ , ∴不妨设
, ∴不妨设 =x,则上式变为10x=3+x,解得x=
=x,则上式变为10x=3+x,解得x= ,即
,即 =
= ;
;∵
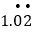 =
=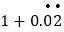 ,设
,设 =x,则上式变为100x=2+x,解得x=
=x,则上式变为100x=2+x,解得x=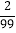 ,
,∴
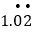 =
=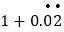 =1+x=1+
=1+x=1+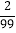 =
=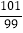
⑴将分数化为小数:
 =______,
=______,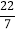 =_______;
=_______;⑵将小数化为分数:
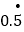 =______,
=______,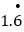 =_______;
=_______;⑶将小数
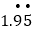 化为分数,需要写出推理过程.
化为分数,需要写出推理过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】梧州市特产批发市场有龟苓膏粉批发,其中A品牌的批发价是每包20元,B品牌的批发价是每包25元,小王需购买A,B两种品牌的龟苓膏粉共1000包.
(1)若小王按需购买A,B两种品牌龟苓膏粉共用22000元,则各购买多少包?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000包龟苓膏粉,共用了y元,设A品牌买了x包,请求出y与x之间的函数关系式;
(3)在(2)中,小王共用了20000元,他计划在网店包邮销售这批龟苓膏粉,每包龟苓膏粉小王需支付邮费8元,若每包销售价格A品牌比B品牌少5元,请你帮他计算,A品牌的龟苓膏粉每包定价不低于多少元时才不亏本?(运算结果取整数)
相关试题

