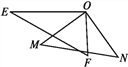
【题目】如图,一副三角板的两个直角顶点重合在一起.
(1)写出∠EOM与∠FON的大小关系,并写出理由;
(2)若∠FON∶∠EON=4∶13,求∠MOF的度数.
参考答案:
【答案】(1)∠EOM=∠FON; (2) 50°.
【解析】试题分析:(1)利用公共角原理可知∠EOM与∠FON相等.(2)设出份数,利用90°关系求出份数,最后可知∠MOF度数.
试题解析:
(1)∠EOM=∠FON.
理由如下:因为∠EOM+∠MOF=∠EOF=90°,
∠FON+∠MOF=∠MON=90°,
所以∠EOM=∠FON.
(2)设∠FON与∠EON的度数分别为4x,13x,
则13x=4x+90°,
解得x=10°,
所以∠FON=4×10°=40°,
所以∠MOF=90°-∠FON=90°-40°=50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在方程0.5x+2y=6中,用含x的代数式表示y,则y=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式y+3>4变形为y>1,这是根据不等式的性质____,不等式两边同时加上___
-
科目: 来源: 题型:
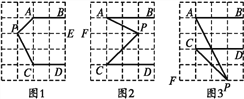
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,已知AB∥CD,分别探讨下面三个图形中∠BAP与∠APC,∠DCP的关系,请任选一个加以说明.
-
科目: 来源: 题型:
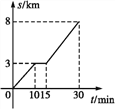
查看答案和解析>>【题目】小明家距离学校8 km,今天早晨,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他增加速度骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行的路程s与他所用的时间t之间的关系.
请根据图象,解答下列问题:
(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明共用了多少时间到学校的?
(3)小明修车前、后的行驶速度各是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟(精确到0.1)?
-
科目: 来源: 题型:
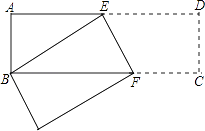
查看答案和解析>>【题目】如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF.求△ABE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=5,BC=12,AB=13,D是BC的中点,求AD的长和△ABD的面积.
相关试题

