【题目】如图,在△ABC中,AC=5,BC=12,AB=13,D是BC的中点,求AD的长和△ABD的面积. 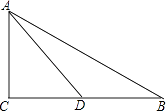
参考答案:
【答案】解:∵在△ABC中,AC=5,BC=12,AB=13, 132=52+122 ,
∴AB2=AC2+CB2 ,
∴△ABC是直角三角形,
∵D是BC的中点,
∴CD=BD=6,
∴在Rt△ACD中,AD= ![]() ,
,
∴△ABD的面积= ![]() ×BD×AC=15.
×BD×AC=15.
【解析】先根据勾股定理的逆定理判断出△ABC的形状,根据中点的定义得到CD的长,根据勾股定理可求出AD的长,再利用三角形的面积公式即可求解.
【考点精析】通过灵活运用勾股定理的概念和勾股定理的逆定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形即可以解答此题.
-
科目: 来源: 题型:
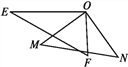
查看答案和解析>>【题目】如图,一副三角板的两个直角顶点重合在一起.
(1)写出∠EOM与∠FON的大小关系,并写出理由;
(2)若∠FON∶∠EON=4∶13,求∠MOF的度数.
-
科目: 来源: 题型:
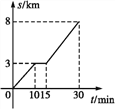
查看答案和解析>>【题目】小明家距离学校8 km,今天早晨,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他增加速度骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行的路程s与他所用的时间t之间的关系.
请根据图象,解答下列问题:
(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明共用了多少时间到学校的?
(3)小明修车前、后的行驶速度各是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟(精确到0.1)?
-
科目: 来源: 题型:
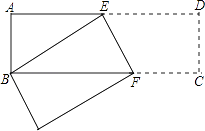
查看答案和解析>>【题目】如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF.求△ABE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个直角三角形的斜边长15cm,一条直角边比另一条直角边长3cm.求两条直角边的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a<b,则a+c____b+c;,若mx>my,且x>y成立,则m___0;若5m-7b>5n-7b,则m__n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+mx﹣8=0的一个实数根为2,则另一实数根及m的值分别为( )
A.4,﹣2
B.﹣4,﹣2
C.4,2
D.﹣4,2
相关试题

