【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论
①a>0,②b>0,③c>0,④b2﹣4ac>0
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】C
【解析】解:①∵该二次函数图象的开口方向向下,
∴a<0;
故本选项错误;
②∵该图象的对称轴x=﹣ ![]() >0,
>0,
∴b>0;
故本选项正确;
③∵该函数图象与y轴交于正半轴,
∴c>0;
故本选项正确;
④该二次函数的图象与x轴有2个不相同的交点,依据根的判别式可知b2﹣4ac>0;
故本选项正确;
综上所述,正确的说法是:②③④,共有3个;
故选C.
【考点精析】认真审题,首先需要了解二次函数图象以及系数a、b、c的关系(二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)).
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下列语句,设适当的未知数,列出二元一次方程:
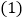 甲数比乙数的
甲数比乙数的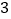 倍少
倍少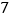 ;
;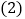 甲数的
甲数的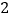 倍与乙数的
倍与乙数的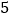 倍的和是
倍的和是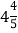 ;
;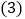 甲数的
甲数的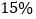 与乙数的
与乙数的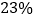 的差是
的差是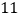 ;
;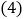 甲数与乙数的和的
甲数与乙数的和的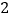 倍比乙数与甲数差的
倍比乙数与甲数差的 多
多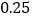 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)【问题提出】
如图①,已知△ABC是等腰三角形,点E在线段AB上,点D在直线BC上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF连接EF
试证明:AB=DB+AF
(2)【类比探究】
如图②,如果点E在线段AB的延长线上,其他条件不变,线段AB,DB,AF之间又有怎样的数量关系?请说明理由
(3)如果点E在线段BA的延长线上,其他条件不变,请在图③的基础上将图形补充完整,并写出AB,DB,AF之间的数量关系,不必说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图1,在以O为原点的平面直角坐标系中,抛物线y=
 x2+bx+c与x轴交于A、B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1,
x2+bx+c与x轴交于A、B两点,与y轴交于点C(0,﹣1),连接AC,AO=2CO,直线l过点G(0,t)且平行于x轴,t<﹣1,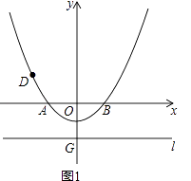
(1)求抛物线对应的二次函数的解析式;
(2)若D为抛物线y= x2+bx+c上一动点,是否存在直线l使得点D到直线l的距离与OD的长恒相等?若存在,求出此时t的值;
x2+bx+c上一动点,是否存在直线l使得点D到直线l的距离与OD的长恒相等?若存在,求出此时t的值;
(3)如图2,若E、F为上述抛物线上的两个动点,且EF=8,线段EF的中点为M,求点M纵坐标的最小值.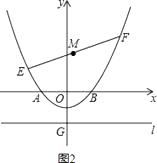
-
科目: 来源: 题型:
查看答案和解析>>【题目】面对资源紧缺与环境保护问题,发展电动汽车成为汽车工业发展的主流趋势.我国某著名汽车制造厂开发了一款新式电动汽车,计划一年生产安装
 辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人:他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:
辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人:他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现: 名熟练工和
名熟练工和 名新工人每月可安装
名新工人每月可安装 辆电动汽车;
辆电动汽车; 名熟练工和
名熟练工和 名新工人每月可安装
名新工人每月可安装 辆电动汽车.
辆电动汽车. 每名熟练工和新工人每月分别可以安装多少辆电动汽车?
每名熟练工和新工人每月分别可以安装多少辆电动汽车? 如果工厂招聘
如果工厂招聘 名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案? 在
在 的条件下,工厂给安装电动汽车的每名熟练工每月发
的条件下,工厂给安装电动汽车的每名熟练工每月发 元的工资,给每名新工人每月发
元的工资,给每名新工人每月发 元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额
元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额 (元)尽可能的少?
(元)尽可能的少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x
﹣1
0
1
3
y
﹣1
3
5
3
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .
相关试题

