【题目】如图,在长方形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,设点
运动,设点![]() 的运动时间为
的运动时间为![]() 秒:
秒:
(1)![]() _________
_________ ![]() .(用
.(用![]() 的代数式表示)
的代数式表示)
(2)当![]() 为何值时,
为何值时, ![]()
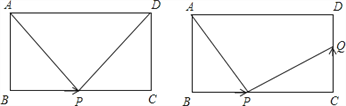
(3)当点![]() 从点
从点![]() 开始运动,同时,点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
开始运动,同时,点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
参考答案:
【答案】(1)10-2t;(2)t=![]() ;(3)
;(3)![]()
【解析】试题分析:(1)根据P点的运动速度可得BP的长,再利用BC-BP即可得到CP的长;
(2)当t=2.5时,△ABP≌△DCP,根据三角形全等的条件可得当BP=CP时,再加上AB=DC,∠B=∠C可证明△ABP≌△DCP;
(3)此题主要分两种情况①当BP=CQ,AB=PC时,△ABP≌△PCQ;当BA=CQ,PB=PC时,△ABP≌△QCP,然后分别计算出t的值,进而得到v的值.
试题解析:(1)点P从点B出发,以2cm/秒的速度沿BC向点C运动,点P的运动时间为t秒时,BP=2t,
则PC=102t;
(2)当t=2.5时,△ABP≌△DCP,
∵当t=2.5时,BP=2.5×2=5,
∴PC=105=5,
∵在△ABP和△DCP中,
AB=DC,∠B=∠C=90°,BP=CP,
∴△ABP≌△DCP(SAS);
(3)①当BP=CQ,AB=PC时,△ABP≌△PCQ,
∵AB=6,
∴PC=6,
∴BP=106=4,
2t=4,
解得:t=2,
CQ=BP=4,
v×2=4,
解得:v=2;
②当BA=CQ,PB=PC时,△ABP≌△QCP,
∵PB=PC,
∴BP=PC=12BC=5,
2t=5,
解得:t=2.5,
CQ=BP=6,
v×2.5=6,
解得:v=2.4.
综上所述:当v=2.4或2时△ABP与△PQC全等。
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列图形,①三角形,②长方形,③平行四边形,④立方体,⑤圆锥,⑥圆柱,⑦圆,⑧球体,其中是平面图形的个数为( )
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
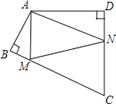
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察以下几组勾股数,并寻找规律:
①3,4,5;
②5,12,13;
③7,24,25;
④9,40,41,…
请你写出有以上规律的第⑤组勾股数:. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市居民日平均用水量的调查
B.对一批LED节能灯使用寿命的调查
C.对重庆新闻频道“天天630”栏目收视率的调查
D.对某校九年级(1)班同学的身高情况的调查 -
科目: 来源: 题型:
查看答案和解析>>【题目】近似数3.1415926用四舍五入法精确到0.001的结果是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年我市有近35000名考生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )
A.每位考生的数学成绩是个体
B.近35000名考生是总体
C.这1000名考生是总体的一个样本
D.1000名考生是样本容量
相关试题

