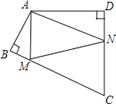
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为_____________.
参考答案:
【答案】120°
【解析】作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值。作DA延长线AH,
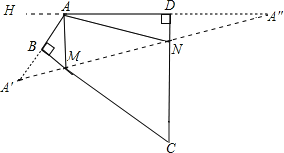
∵∠DAB=120°,
∴∠HAA′=60°,
∴∠AA′M+∠A″=∠HAA′=60°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A'=2(∠AA′M+∠A')=2×60°=120°。
故答案为:120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ΔABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D、E两点,并连接BD、DE.若∠A=30°,AB=AC,则∠BDE的度数为( )
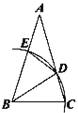
A. 67.5° B. 52.5° C. 45° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(11,m)在第6段抛物线C6上,则m= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列图形,①三角形,②长方形,③平行四边形,④立方体,⑤圆锥,⑥圆柱,⑦圆,⑧球体,其中是平面图形的个数为( )
A. 5个 B. 4个 C. 3个 D. 2个
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察以下几组勾股数,并寻找规律:
①3,4,5;
②5,12,13;
③7,24,25;
④9,40,41,…
请你写出有以上规律的第⑤组勾股数:. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,
中, 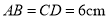 ,
, 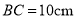 ,点
,点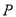 从点
从点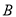 出发,以
出发,以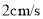 的速度沿
的速度沿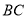 向点
向点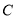 运动,设点
运动,设点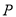 的运动时间为
的运动时间为 秒:
秒: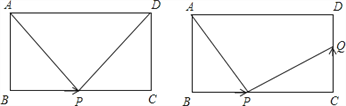
(1)
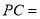 _________
_________ 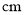 .(用
.(用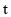 的代数式表示)
的代数式表示)(2)当
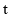 为何值时,
为何值时, 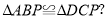
(3)当点
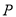 从点
从点 开始运动,同时,点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
开始运动,同时,点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市居民日平均用水量的调查
B.对一批LED节能灯使用寿命的调查
C.对重庆新闻频道“天天630”栏目收视率的调查
D.对某校九年级(1)班同学的身高情况的调查
相关试题

