【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克,为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天的房租等固定成本共24元,设每千克降价x元每天销量为y千克.
(1)求y与x的函数关系式;
(2)如何定价,才能使每天获得的利润为200元,且使每天的销量较大?
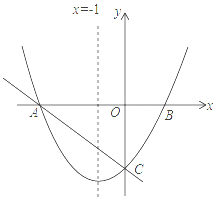
参考答案:
【答案】(1)y=200+400x;
(2)应将每千克小型西瓜的售价定为2.7元/千克.
【解析】试题分析:(1)根据这种小型西瓜每降价0.1元/千克,每天可多售出40千克可直接得出y与x的函数关系式;(2)设应将每千克小型西瓜的售价降低x元.那么每千克的利润为:(3-2-x),由于这种小型西瓜每降价O.1元/千克,每天可多售出40千克.所以降价x元,则每天售出数量为:200+![]() 千克.本题的等量关系为:每千克的利润×每天售出数量-固定成本=200.
千克.本题的等量关系为:每千克的利润×每天售出数量-固定成本=200.
试题解析:(1)∵每千克降价x元每天销量为y千克,
∴y=200+![]() ,即y=200+400x;
,即y=200+400x;
(2)设应将每千克小型西瓜的售价降低x元.
根据题意,得[(3﹣2)﹣x](200+![]() )﹣24=200.
)﹣24=200.
原式可化为:50x2﹣25x+3=0,
解这个方程,得x1=0.2,x2=0.3.
为使每天的销量较大,应降价0.3元,即定价2.7元/千克.
答:应将每千克小型西瓜的售价定为2.7元/千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个多边形的每个外角都为30°,则这个多边形是( )
A. 十二边形 B. 十边形 C. 八边形 D. 六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④
 <a<
<a< ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )
A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:(1)(x﹣1)(x+3)=12;(2)(x﹣3)2=3﹣x;(3)3x2+5(2x+1)=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(5,6)与点B关于x轴对称,则点B的坐标为( )
A. (5,6) B. (-5,-6) C. (-5,6) D. (5,-6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程(m﹣3)x2+2mx+m+1=0有两个不相等的实数根,并且这两个根又不互为相反数.
(1)求m的取值范围;
(2)当m在取值范围内取最小正偶数时,求方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中的真命题是( )
A.在所有连接两点的线中直线最短
B.经过两点有且只有一条直线
C.内错角互补则两直线平行
D.空间中,如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直
相关试题

