Question

【题目】如图，在Rt△ABC中，∠ACB=90°，点D、F分别在AB、AC上，CF=CB，连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．

（1）求证：△BCD≌△FCE；
（2）若EF∥CD，求∠BDC的度数．

Answer 1

【答案】
（1）证明：∵将线段CD绕点C按顺时针方向旋转90°后得CE，

∴CD=CE，∠DCE=90°，

∵∠ACB=90°，

∴∠BCD=90°﹣∠ACD=∠FCE，

在△BCD和△FCE中，

，

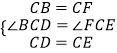∴△BCD≌△FCE（SAS）

（2）解：由（1）可知△BCD≌△FCE，

∴∠BDC=∠E，∠BCD=∠FCE，

∴∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°，

∵EF∥CD，

∴∠E=180°﹣∠DCE=90°，

∴∠BDC=90°

【解析】（1）由旋转的性质可得：CD=CE，再根据同角的余角相等可证明∠BCD=∠FCE，再根据全等三角形的判定方法即可证明△BCD≌△FCE；（2）由（1）可知：△BCD≌△FCE，所以∠BDC=∠E，易求∠E=90°，进而可求出∠BDC的度数．