【题目】三角形两边的长分别是8和6,第3边的长是一元二次方程x2﹣16x+60=0的一个实数根,则该三角形的面积是 .
参考答案:
【答案】24或8 ![]()
【解析】解:∵x2﹣16x+60=0, ∴(x﹣6)(x﹣10)=0,
解得:x1=6,x2=10,
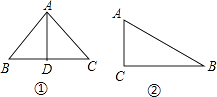
当x=6时,则三角形是等腰三角形,如图①:AB=AC=6,BC=8,AD是高,
∴BD=4,AD= ![]() =2
=2 ![]() ,
,
∴S△ABC= ![]() BCAD=
BCAD= ![]() ×8×2
×8×2 ![]() =8
=8 ![]() ;
;
当x=10时,如图②,AC=6,BC=8,AB=10,
∵AC2+BC2=AB2 ,
∴△ABC是直角三角形,∠C=90°,
S△ABC= ![]() BCAC=
BCAC= ![]() ×8×6=24.
×8×6=24.
∴该三角形的面积是:24或8 ![]() .
.
所以答案是:24或8 ![]() .
.
【考点精析】通过灵活运用因式分解法和等腰三角形的性质,掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;等腰三角形的两个底角相等(简称:等边对等角)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
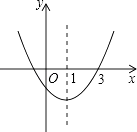
A.abc<0
B.4ac﹣b2<0
C.a﹣b+c<0
D.2a+b<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
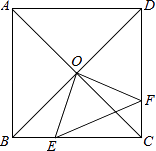
A.
B.
C.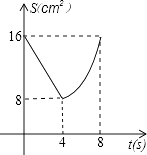
D.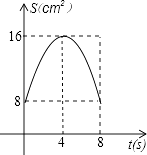
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为 , 则图中阴影部分的面积是 .
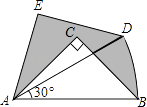
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为6的正三角形纸片
 按如下顺序进行两次折叠,展开后,得折痕
按如下顺序进行两次折叠,展开后,得折痕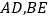 (如图①),
(如图①),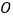 为其交点.
为其交点.(1)探求
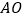 与
与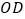 的数量关系,并说明理由;
的数量关系,并说明理由;(2)如图②,若
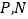 分别为
分别为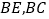 上的动点.
上的动点.①当
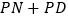 的长度取得最小值时,求
的长度取得最小值时,求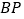 的长度;
的长度;②如图③,若点
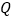 在线段
在线段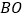 上,
上,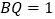 ,则
,则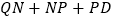 的最小值为 .
的最小值为 .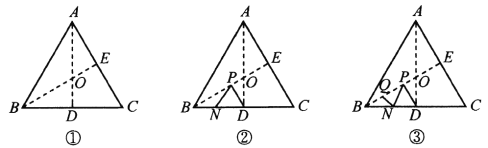
-
科目: 来源: 题型:
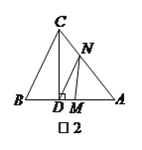
查看答案和解析>>【题目】如图
 ,
,  中,
中,  于
于 ,且
,且 .
.(
 )试说明
)试说明 是等腰三角形.
是等腰三角形.(
 )已知
)已知 ,如图
,如图 ,动点
,动点 从点
从点 出发以每秒
出发以每秒 的速度沿线段
的速度沿线段 向点
向点 运动,同时动点
运动,同时动点 从点
从点 出发以相同速度沿线段
出发以相同速度沿线段 向点
向点 运动,当其中一点到达终点时整个运动都停止.设点
运动,当其中一点到达终点时整个运动都停止.设点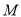 运动的时间为
运动的时间为 (秒).
(秒).①若
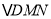 的边与
的边与 平行,求
平行,求 的值.
的值.②若点
 是边
是边 的中点,问在点
的中点,问在点 运动的过程中,
运动的过程中,  能否成为等腰三角形?若能,求出
能否成为等腰三角形?若能,求出 的值;若不能,请说明理由.
的值;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
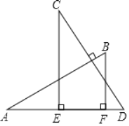
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
相关试题

