【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?

解:a与c平行;
理由:因为∠1=∠2(____)
所以a//b(_______________)
因为∠3=∠4 (________)
所以b//c(_____________)
所以a//c(_____________)
参考答案:
【答案】已知 同位角相等,两直线平行 已知 同位角相等,两直线平行 平行于同一条直线的两条直线平行
【解析】a∥c,理由如下:
∵∠1=∠2(已知),
∴a//b(同位角相等,两直线平行),
∵∠3=∠4 (已知),
∴b//c(同位角相等,两直线平行),
∴a//c(平行于同一条直线的两条直线平行).
故答案为已知;同位角相等,两直线平行;已知;同位角相等,两直线平行;平行于同一条直线的两条直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩(满分为100分)如图所示.(方差公式:s2=
 [(x1﹣
[(x1﹣  )2+(x2﹣
)2+(x2﹣  )2+…+(xn﹣
)2+…+(xn﹣  )2])
)2]) 
(1)根据图示填写表格单位(分);平均数/分
中位数/分
众数/分
初中代表队
85
高中代表队
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好?
(3)计算两队决赛成绩的方差判断哪一个代表队选手成绩较为稳定. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.6a﹣5a=1B.a2a3=a5C.a6÷a3=a2D.(a2)3=a5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
解:a与c平行.
理由:因为∠1=∠2( ),
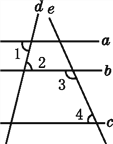
所以a∥b ( ).
因为∠3+∠4=180°( ),
所以b∥c ( ).
所以a∥c ( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE、CF.
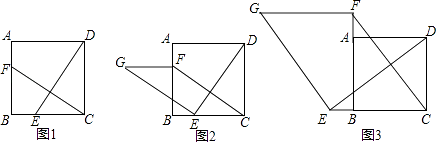
(1)求证:DE=CF;
(2)在(1)条件下,如图2,过点E作BG⊥DE,且EG=DE,连接FG,试判断:FG与CE的数量关系和位置关系?给出证明.
(3)如图3,若点E、F分别是CB、BA的延长线上的点,其他条件不变,(2)中结论是否仍然成立?请直接写出你的判断.
相关试题

