【题目】如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE、CF. 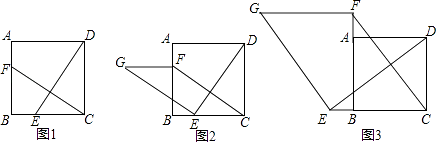
(1)求证:DE=CF;
(2)在(1)条件下,如图2,过点E作BG⊥DE,且EG=DE,连接FG,试判断:FG与CE的数量关系和位置关系?给出证明.
(3)如图3,若点E、F分别是CB、BA的延长线上的点,其他条件不变,(2)中结论是否仍然成立?请直接写出你的判断.
参考答案:
【答案】
(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
在△CBF和△DCE中, 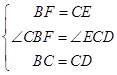 ,
,
∴△CBF≌△DCE(SAS),
∴CF=DE;
(2)解:结论:GF=EC,GF∥EC,
理由:由(1)知,∠BCF=∠CDE,
∵∠BCF+∠DCF=90°,
∴∠CDE+∠DCF=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形,
∴GF=EC,GF∥EC;
(3)解:结论仍然成立,GF=EC,GF∥EC,
理由:由(1)知,∠BCF=∠CDE,
∵∠BCF+∠DCF=90°,
∴∠CDE+∠DCF=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形,
∴GF=EC,GF∥EC.
【解析】(1)由正方形的性质得出BC=CD,∠ABC=∠DCE=90°,进而判断出△CBF≌△DCE(SAS),即可得出结论;(2)先判断出CF⊥DE,进而判断出EG∥CF,即可判断出四边形EGFC是平行四边形,即可得出结论;(3)同(1)的方法即可得出结论.
【考点精析】本题主要考查了平行四边形的判定与性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?

解:a与c平行;
理由:因为∠1=∠2(____)
所以a//b(_______________)
因为∠3=∠4 (________)
所以b//c(_____________)
所以a//c(_____________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
解:a与c平行.
理由:因为∠1=∠2( ),
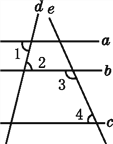
所以a∥b ( ).
因为∠3+∠4=180°( ),
所以b∥c ( ).
所以a∥c ( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠E=∠F,∠B=∠C,AE=AF,以下结论:①∠FAN=∠EAM;②EM=FN;
③△ACN≌△ABM;④CD=DN.其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx﹣1一定经过点( )
A.(1,0)
B.(1,k)
C.(0,k)
D.(0,﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】将6﹣(+3)﹣(﹣7)+(﹣2)写成省略加号的和的形式为( )
A.﹣6﹣3+7﹣2
B.6﹣3﹣7﹣2
C.6﹣3+7﹣2
D.6+3﹣7﹣2
相关试题

