【题目】如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( )
A.(2,﹣3)
B.(2,3)
C.(3,2)
D.(3,﹣2)
参考答案:
【答案】C
【解析】解:∵点A坐标为(0,a),
∴点A在该平面直角坐标系的y轴上,
∵点C、D的坐标为(b,m),(c,m),
∴点C、D关于y轴对称,
∵正五边形ABCDE是轴对称图形,
∴该平面直角坐标系经过点A的y轴是正五边形ABCDE的一条对称轴,
∴点B、E也关于y轴对称,
∵点B的坐标为(﹣3,2),
∴点E的坐标为(3,2).
故选:C.
由题目中A点坐标特征推导得出平面直角坐标系y轴的位置,再通过C、D点坐标特征结合正五边形的轴对称性质就可以得出E点坐标了.本题考查了平面直角坐标系的点坐标特征及正五边形的轴对称性质,解题的关键是通过顶点坐标确认正五边形的一条对称轴即为平面直角坐标系的y轴.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )

A.50°
B.51°
C.51.5°
D.52.5° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F B. BC∥EF C. ∠A=∠EDF D. AD=CF
-
科目: 来源: 题型:
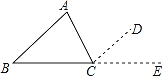
查看答案和解析>>【题目】已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
解:∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∵∠ACD=∠ (已作)
AB∥CD( )
∴∠B= ( )
而∠ACB+∠ACD+∠DCE=180°
∴∠ACB+ + =180°( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于不等式组
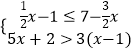 下列说法正确的是( )
下列说法正确的是( )
A.此不等式组无解
B.此不等式组有7个整数解
C.此不等式组的负整数解是﹣3,﹣2,﹣1
D.此不等式组的解集是﹣ <x≤2
<x≤2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.
(1)△BEM与△AEC全等吗?请说明理由;
(2)BM与AC相等吗?请说明理由;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2﹣2
 x+1与坐标轴的交点个数是( )
x+1与坐标轴的交点个数是( )
A.0
B.1
C.2
D.3
相关试题

