【题目】已知:如图所示,△ABC中,∠ABC=45°,高AE与高BD交于点M,BE=4,EM=3.
(1)△BEM与△AEC全等吗?请说明理由;
(2)BM与AC相等吗?请说明理由;
(3)求△ABC的面积.

参考答案:
【答案】(1)全等,理由见解析;(2)相等,理由见解析;(3)S△ABC=14.
【解析】
(1)根据已知条件易证AE=BE,再由AAS即可证明△BEM≌△AEC;(2)根据全等三角形的性质即可得BM=AC;(3)由(1)可知△BEM≌△AEC,根据全等三角形的性质可得BE=AE,EM=EC,再由三角形的面积公式计算即可.
(1)全等,
∵AE、BD为△ABC的高,
∴∠BEM=∠AEC=∠BDC=90°,
∴∠EBM+∠C=∠EBM+∠BME=90°,
∴∠BME=∠C,
又∠ABC=45°,
∴∠ABC=∠BAE=45°,
∴AE=BE,
在△BEM和△AEC中
∵
∴△BEM≌△AEC(AAS),
(2)相等,
∵△BEM≌△AEC,
∴BM=AC.
(3)∵△BEM≌△AEC,
∴BE=AE=4,EM=EC=3,
∴BC=BE+EC=7,
∴S△ABC=![]() ×7×4=14.
×7×4=14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
解:∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∵∠ACD=∠ (已作)
AB∥CD( )
∴∠B= ( )
而∠ACB+∠ACD+∠DCE=180°
∴∠ACB+ + =180°( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( )

A.(2,﹣3)
B.(2,3)
C.(3,2)
D.(3,﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】对于不等式组
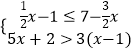 下列说法正确的是( )
下列说法正确的是( )
A.此不等式组无解
B.此不等式组有7个整数解
C.此不等式组的负整数解是﹣3,﹣2,﹣1
D.此不等式组的解集是﹣ <x≤2
<x≤2 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2﹣2
 x+1与坐标轴的交点个数是( )
x+1与坐标轴的交点个数是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点选择180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( )
A.y=﹣(x﹣ )2﹣
)2﹣ 
B.y=﹣(x+ )2﹣
)2﹣ 
C.y=﹣(x﹣ )2﹣
)2﹣ 
D.y=﹣(x+ )2+
)2+ 
相关试题

