【题目】填空:把下面的推理过程补充完整,并在括号内注明理由,
如图,已知△ABC中,E、F分别是AB、AC上的两点,且EF∥BC,D为EF上一点,且BD=CD,ED=FD,请说明BE=CF.
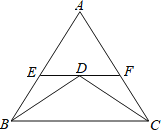
解:∵BD=CD(已知)
∴∠DBC=∠DCB(______)
∵EF∥BC(已知)
∴∠EDB=∠DBC
∠FDC=______(______)
∴∠EDB=∠FDC(等量代换)
在△EBD和△FCD中,
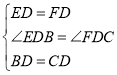
∴△EBD≌△FCD(______)
∴BE=CF(______)
参考答案:
【答案】等边对等角;∠DCB;两直线平行,内错角相等;SAS;全等三角形的对应边相等
【解析】
根据SAS、等腰三角形的性质、平行线的性质证明两个三角形全等即可.
解:∵BD=CD(已知)
∴∠DBC=∠DCB(等边对等角)
∵EF∥BC(已知)
∴∠EDB=∠DBC
∠FDC=∠DCB(两直线平行,内错角相等)
∴∠EDB=∠FDC(等量代换)
在△EBD和△FCD中,
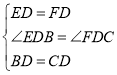 ,
,
∴△EBD≌△FCD(SAS)
∴BE=CF(全等三角形的对应边相等),
故答案为:等边对等角;∠DCB;两直线平行,内错角相等;SAS;全等三角形的对应边相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人玩“石头、剪刀、布”的游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“石头”、“剪刀”、“布”的卡片张数分别为3、5、7.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种卡片不分胜负
(1)若甲先摸,则他摸出“石头”的概率是______;
(2)若甲先摸出“石头”,则乙再摸出“石头”的概率是______;
(3)若甲先摸出了“石头”,则乙获胜的概率是______;
(4)若甲先摸,则他摸出哪种卡片获胜的可能性最大?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市郊外景区内一条笔直的公路a经过三个景点A、B、C,景区管委会又开发了风景优美的景点D,经测量景点D位于景点A的北偏东30°方向8km处,位于景点B的正北方向,还位于景点C的北偏西75°方向上,已知AB=5km.

(1)景区管委会准备由景点D向公路a修建一条距离最短的公路,不考虑其它因素,求出这条公路的长;(结果精确到0.1km)
(2)求景点C与景点D之间的距离.(结果精确到1km)
(参考数据:
 =1.73,
=1.73, =2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.)
=2.24,sin53°=cos37°=0.80,sin37°=cos53°=0.60,tan53°=1.33,tan37°=0.75,sin38°=cos52°=0.62,sin52°=cos38°=0.79,tan38°=0.78,tan52°=1.28,sin75°=0.97,cos75°=0.26,tan75°=3.73.) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 中,
中, ,点
,点 为
为 边上一点,连接BD,点
边上一点,连接BD,点 为
为 上一点,连接
上一点,连接 ,
, ,过点
,过点 作
作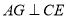 ,垂足为
,垂足为 ,交
,交 于点
于点 .
.(1)求证:
 ;
;(2)如图2,若
 ,点
,点 为
为 的中点,求证:
的中点,求证: ;
;(3)在(2)的条件下,如图3,若
 ,求线段
,求线段 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】东方专卖店专销某种品牌的钢笔,进价12元/支,售价20元/支.为了促销,专卖店决定凡是买10支以上的,每多买一支,售价就降低0.10元(例如,某人买20支钢笔,于是每只降价0.10×(20﹣10)=1元,就可以按19元/支的价格购买),但是最低价为16元/支.
(1)求顾客一次至少买多少支,才能以最低价购买?
(2)写出当一次购买x支时(x>10),利润y(元)与购买量x(支)之间的函数关系式;
(3)有一天,一位顾客买了46支,另一位顾客买了50支,专实店发现卖了50支反而比卖46支赚的钱少,为了使每次卖的多赚钱也多,在其他促销条件不变的情况下,最低价16元/支至少要提高到多少,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车制造厂开发一款新式电动汽车,计划一年生产安装
 辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:
辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现: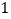 名熟练工和
名熟练工和 名新工人每月可安装
名新工人每月可安装 辆电动汽车;
辆电动汽车; 名熟练工和
名熟练工和 名新工人每月可安装
名新工人每月可安装 辆电动汽车.
辆电动汽车.(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘
 名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,
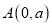 、
、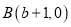 ,且
,且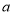 、
、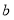 满足
满足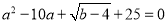
(1)求
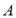 、
、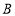 两点的坐标;
两点的坐标;(2)过点
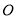 的直线
的直线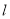 上有一点
上有一点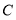 ,连接
,连接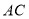 、
、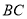 ,
,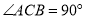 ,如图2,当点
,如图2,当点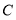 在第二象限时,
在第二象限时,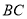 交
交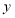 轴于点
轴于点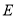 ,延长
,延长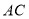 交
交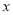 轴于点
轴于点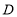 ,设
,设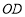 的长为
的长为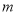 ,
,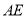 的长为
的长为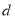 ,用含
,用含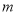 的式子表示
的式子表示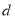 ;
;(3)在(2)的条件下,如图3,当点
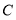 在第一象限时,过点
在第一象限时,过点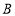 作
作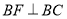 交
交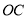 于点
于点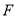 ,连接
,连接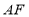 ,若
,若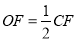 ,
,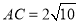 ,求
,求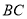 的长.
的长.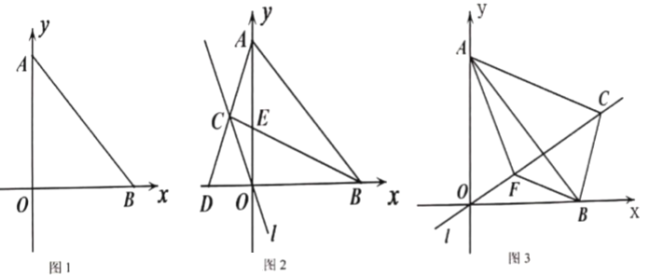
相关试题

