[题目]将正偶数按下表排成列:第一列第二列第三列第四列第五列第一行2468第二行16141210第三行18202224第四行32302826根据上表排列规律.则偶数应在第列．题目和参考答案 ——青夏教育精英家教网—

【题目】将正偶数按下表排成列：

	第一列	第二列	第三列	第四列	第五列
第一行		2	4	6	8
第二行	16	14	12	10
第三行		18	20	22	24
第四行	32	30	28	26

根据上表排列规律，则偶数应在第_________列．

参考答案：

【答案】三

【解析】

根据题意得到每一行是4个偶数，奇数行从第2列往后排，偶数行从第4列往前排，然后用2000除以2得到2000是第1000个偶数，再用1000÷4得250，于是可判断2000在第几行第几列．

∵2020÷2=1010，

∴2020是第1010个偶数，

而1010÷4=252······2，

第1010个偶数是253行第二个数，

253为奇数，则从第二列往右数，

∴第1010个偶数是253行，第三列，

则偶数应在第三列，

故答案为三.

相关试题

科目： 来源： 题型：

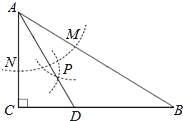
【题目】如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P，连结AP并延长交BC于点D，则下列说法中正确的个数是（　　）
①AD是∠BAC的平分线；②∠ADC=60°；③点D在AB的中垂线上；④S△DAC：S△ABC=1：3．
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目： 来源： 题型：

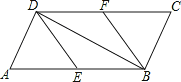
【题目】如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线．
（1）求证：△ADE≌△CBF；
（2）若∠ADB是直角，则四边形BEDF是什么四边形？证明你的结论．
查看答案和解析>>
科目： 来源： 题型：

【题目】我国是世界上严重缺水的国家之一．为了倡导“节约用水从我做起”，小刚在他所在班的50名同学中，随机调查了10名同学家庭中一年的月均用水量（单位：t），并将调查结果绘成了如下的条形统计图
【1】求这10个样本数据的平均数、众数和中位数；
【2】根据样本数据，估计小刚所在班50名同学家庭中月均用水量不超过7 t的约有多少户．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在△ABC中，∠BAC=90°，AB=4，AC=6，点D、E分别是BC．AD的中点，AF∥BC交CE的延长线于F．则四边形AFBD的面积为______．
查看答案和解析>>
科目： 来源： 题型：

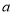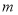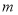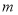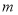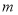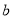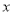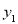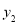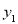【题目】为发展旅游经济，我市某景区对门票釆用灵活的售票方法吸引游客．门票定价为50元/人，非节假日打折售票，节假日按团队人数分段定价售票，即人以下（含人）的团队按原价售票；超过人的团队，其中人仍按原价售票，超过人部分的游客打折售票．设某旅游团人数为人，非节假日购票款为（元），节假日购票款为（元）．与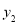之间的函数图象如图所示．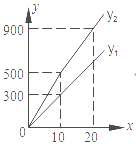
（1）观察图象可知：　　；　　；　　；
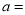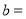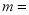（2）直接写出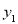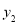，与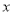之间的函数关系式；
（3）某旅行社导游王娜于5月1日带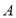团，5月20日（非节假日）带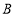团都到该景区旅游，共付门票款1900元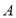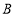，，两个团队合计50人，求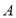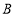，两个团队各有多少人？
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，∠AOB=10°，点P在OB上．以点P为圆心，OP为半径画弧，交OA于点P1（点P1与点O不重合），连接PP1；再以点P1为圆心，OP为半径画弧，交OB于点P2（点P2与点P不重合），连接P1 P2；再以点P2为圆心，OP为半径画弧，交OA于点P3（点P3与点P1不重合），连接P2 P3；……
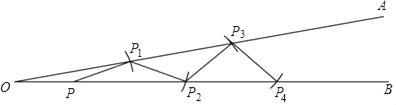
请按照上面的要求继续操作并探究：
∠P3 P2 P4=_____°；按照上面的要求一直画下去，得到点Pn，若之后就不能再画出符合要求点Pn+1了，则n=_____．
查看答案和解析>>